Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
If you have been following AI Factory's activities over the last few years, you will have noticed that our card game "Spades Free" has consumed a dominant proportion of our AI work. With this in mind it makes sense to talk more about Spades and in this article we indeed explain our important Spades play inference system.
With imperfect information games it is tempting to work with pure random game states (e.g. random card deals) in order to determine what game state should be explored. However in our Spades we have a finely balanced inference system that can examine plays and infer what cards each player might have from plays made. This is used as a base from which to analyse the game state to be searched.
This system is actually quite attractive as the coding decisions to implement it map very closely to how a human player might think.
Background
First we need to establish how our program works. From Searching the Unknown with MCTS you will see that the version of Monte Carlo Tree Search (MCTS) we use is Information Set MCTS (ISMCTS), where before each search rollout the cards are re-dealt (a determinisation). So each of the thousands of search rollouts will be using a different card deal. The tree that is grown from this is mostly populated by illegal plays for any possible deal, with up to 50 or so branches per node, far more than there are legal moves in any one hand. This slightly odd method builds a probability tree rather than an exact search tree, so that any move inside this tree that is higher rated, simply means that it is more likely to lead to a better outcome, even though illegal in most search rollouts.
For those unfamiliar with MCTS, the final non-intuitive outcome is that the best move is simply the one most explored. Unlike Minimax, there is no evaluation delivered by the search, just a search count.
The reader is again referred back to the referenced article above, which explains MCTS and ISMCTS in the context of comparing it to Minimax.

Inference-free Search?
The simplest idea before a search rollout would be to simply take all legal cards, other than those already played or held by the player to play, and deal these randomly to the other players. This would work, but throws away some critical cheap information. Our own inference system is subtle, but there are already rock solid inferences there that can be made for free, as follows:
| (1) | If a player does not follow suit, we immediately know that that player has no cards of that suit, so cannot in the future be dealt cards of that suit. All players get to see this. | ||
| (2) | (Of course) cards already played or held by player, are not available. | ||
This is obvious, and important and cheap, but not consequence free. If you take this and do a simple randomised deal you will many times find you are only left with cards that a recipient player cannot hold. To avoid this you need to deal cards that can only be dealt to a subset of players first, so cards where only one player can hold that card, followed by 2 players etc. Even that can fail, in which case a deal needs to be junked and re-tried. A further issue is that in some exotic distributions this may endlessly fail, in which case it is practically better to proceed with one of the failed deals!
Supporting Inference across 4 players with just TRUE/FALSE chance of card ownership
To support the simple situation above, you only need a simple data structure that provides a map of true/false for every card for every player, indicating who might have that card. E.g.
// iProbability [player] [card] Bool iProbability[4][52]; // indexed by 4 players and 52 cards
So each card has 4 probabilities, in this case effectively 0% and 100%. This limited structure is possible as all players have the same information.
However our system allows a range of probabilities 0% to 100%, where each player may have different information.
Supporting Subtle Inference across 4 players with 0%-100% chance of ownership
A player can infer from an opponent or partner play, but the situation is not the same as other players, as each player also sees their own cards, so each have different context information. This requires a bigger structure:
// iProbability [this player] [other players] [cards] int iProbability[4][4][52]; // indexed by 4x players, 4x players and 52 cards
So any one card has 16 possible probabilities. Of these 25% will generally be 0% or 100%, where both player indexes are the same. E.g. iProbability[North][North][x] is North's view of North's hand, where North has complete information.
This probability array directly after the deal will be populated by 0%, 33% or 100% values, as shown in figure.1 below. 33% is derived simply from the fact that for any one player, a card they do not hold has a 33% chance of being held by one of the other 3 players.

Figure 1 Probability tables for just player East after the first deal
In this layout the grey backlit figures show where that player actually possesses that card. Squares marked "-" mean 0% and "##" means 100%. In the deal table below the current deal is shown in cyan, indicating -1 meaning "no bid made yet".
How are inferences made?
In the tables above each player's projection of a card's probability starts at 33.33% and these 3 probabilities add up to 100%. If an inference is made then a single probability adjusted by (say) increasing it by 25%, causing the other 2 probabilities to automatically reduce. So 33% becomes 42% (rounded), which means the other two 33% probabilities both reduce to 29%. So any adjustment is always made on a single card for a single player and corresponding adjustments are then automatically made for the same card for the two other players.
These other two player probabilities for adjustment are adjusted in proportion so, for example, increasing the target probability of 33% by 50%, where the other players are already 13% and 53% will not reduce the 13% to zero, but weight the two drops by reducing to 3.25% and 13.5% respectively.
This auto-balancing simplified the complete system. The engine code need only request a single adjustment to a single card probability for one player and the system handles any other needed adjustments. Note if a probability decreases then the probability of other players holding that card goes up. Eventually one such probability might rise to 100%, at which point we are certain that player has that card.
Note also that a probability adjustment may not just be +/- some percentage change, but a change such as "this player does/doesn't have this card".
Where can we make inferences?
Ok we have a supporting structure, so what it is we can do? Human players watch cards being played and draw conclusions and the same applies to a computer player. This starts before trick play at bidding. If a player bids 1, then you know they very probably have a weak hand. For example in figure 2 below we show all four sets of tables for each of the players, showing their separate probability maps. The actual bids made are shown below the player name. So at this point trick play is just about to start.

Figure 2 All four Player probability tables after the dealing phase
Examining this table you can see significant differences in estimations by each player of who has what card. For example East thinks that North has an 80% chance of holding the AS whereas player South estimates this at just 50%.
The reason for this disparity is that South has a very weak hand but knows North bid 6 and West 2 and East 3. South could well imagine that East might hold AS, although North is more likely. East however knows it does not have the AS, and sees West 2 and South 1, and from that believes it is very likely that North holds this card.
The bidding is critical as in this case it is important to realise that North (bid 6) must have a strong hand, whereas South (bid 1) must be weak. If you look at East and West's probability tables in the middle of figure 2, you can see that both see South as weak, with few expected trumps, whereas North has many.
This highlights an apparent weakness. It can be seen that the sum of all percentages for South are less than for North, which implies that South has "fewer" cards. The auto-balancing of individual card probability changes only handles that single card for 3 players and does not try to assume the player's other totals need to be adjusted. To do this card-by-card would be absurdly expensive, so what actually happens is that when these tables are used that the probabilities are copied and adjusted so that each player is seen to have a similar net share of card probabilities.
How is this used by the randomised deals? (Determinisation)
We need to know how this is used by the search. The method is relatively simple. Again in the simple deal structure first described, cards that can only fit in a single or pair of player's hand are dealt first. However rather than a simple equal split between each player, the recipient of the card is calculated by summing the probabilities of all recipients. E.g.
North 60% + South 35% + East 33% = 128% (?)
The chance that North gets this card is then 60/128. Note! Counter to intuition, these probabilities do not necessarily add up to 100%! Although in the raw tables they do, note that the probability tables are scaled just before determinisation so that the sum of all probabilities for each player comes to the same total, so that all players are dealt cards at the same rate. Without this adjustment, one player may get many of their cards early and another left with the cards dealt later. The latter would likely to leave a skew with players being forced to take cards that they are unlikely to have held.
Trick play Inferences
This is where the scope for inference rapidly expands as so many plays offer the opportunity for making a player inference. This happens during playmove and is the part of the program most closely tied to the thinking of a human player. The code that implements this closely follows natural human thinking.
Examples of these inferences include:
| 1. | Nil bid defender playing X has no higher card that does not win trick | |
| 2. | If Nil player plays a Spade then likely he has no other Spades | |
| 3. | Player did not follow suit and needs tricks. Very probably has no higher cards of same suit of card played | |
| 4. | Player did not trump. Weakly assume no trumps, depending on value of card, unless player went Nil | |
| 5. | If played card low not following suit then probably no lower cards in same suit (probably voiding suit) | |
| 6. | Player wins trick but already has too many tricks. User probably has no choice. i.e. has no lower cards | |
| 7. | Player wins trick and needs tricks. User probably has no higher cards in same suit | |
| 8. | Card is not top, we followed suit, losing but still need tricks. Probably no higher cards | |
| 9. | Card is not top card and we followed suit. We probably have no higher winning cards, if we need tricks | |
| 10. | Card is not top, but partnership winning trick and do not want tricks. Probably no higher cards |
The above also has some sub-variants, but this is a flavour of the nature of the inferences used. Note that different value cards will have different levels of inference change.
Let's jump into a later stage in the same game above to see this at work. See figure 3 below:

Figure 3 The probabilities for East after many cards have been played
Here you can see that the probability table is now quite sparse. Each player now has either 2 or 3 cards left to play. Note the actual locations of cards are shown in backlit grey. In an ideal world these would all register 100%, but that is simply not possible because we do not have that level of information, except for rare situations at the end of the game where the positions of all cards can be exactly deduced.
However it can be seen that the table performs quite well, with projected cards generally with high percentages. The mean percentage per actual correctly projected card is an average 49.6%, compared to 31.1% mean for incorrect cards, so the projected probabilities are meaningful.
If you look at the figures you can also see that the probabilities are not part of simple gradients. Note East's club projections for West, where 4C is 77% and 8C is dropped to just 18%, but TC is back up at 51%.
We can find out why this is by examining the game. In particular why East thinks West has 4C (which it does).
Inferences when South earlier plays 6C
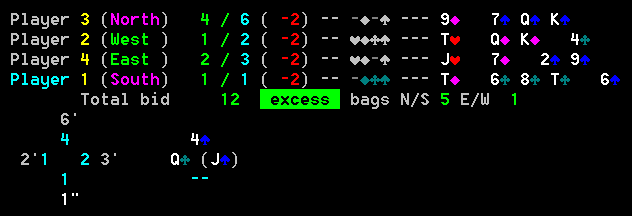
Figure 4 Position just before South plays 6C
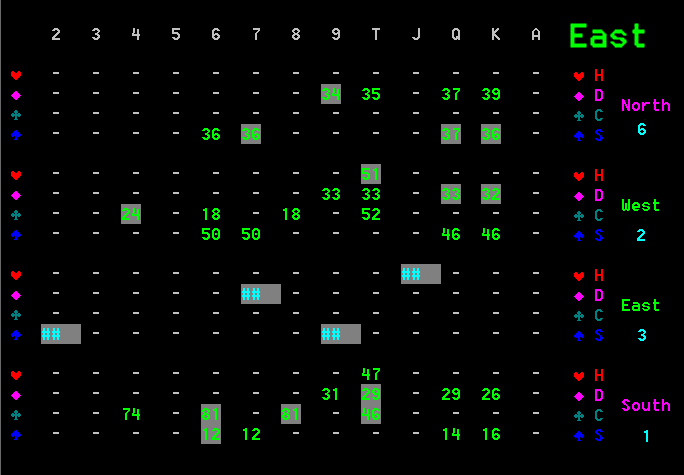
Figure 5 East's probability table before South Play 6C
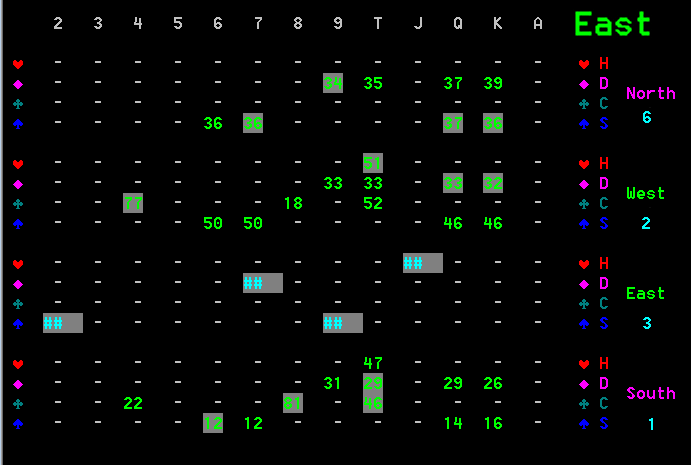
Figure 6 East's probability table after South plays 6C
Looking at the inference change we see that after South played 6C that East's view of West chances of holding 4C has dramatically increased from 24% to 77%. The driving inference that caused this was:
| 4C is lower than card 6C played. Strong inference that South does not have 4C, otherwise South would have played it instead of 6C. |
The impact of this is that East's view of South's probability of holding 4C is reduced from 74% to 22%. That means that someone else must have it. East knows it is void in clubs and that North is also void, so the probability is moved to West.
Key to this is that the dramatic change in West probability was not the product of a West play, but the indirect balancing consequence of a play by South.
We could show many other such examples, but the above shows the principle, so we can now instead assess the actual play impact.
How does inferences accuracy vary throughout the game?
At the start of play it is pretty well impossible to make many trick play inferences as so little is known. In the game above we can monitor the accuracy of probability projections by plotting the average error of each card prediction during the game. Note that (for example) the errors for West might be significantly different than North as they are working with different base information.
However such a plot would reveal limited general information about the general error per projection in regular play, so figure 7 below instead plots an average for 10 hands, so that each value is actually an average error over 40 values (10 hands x (N+W+E+S)).
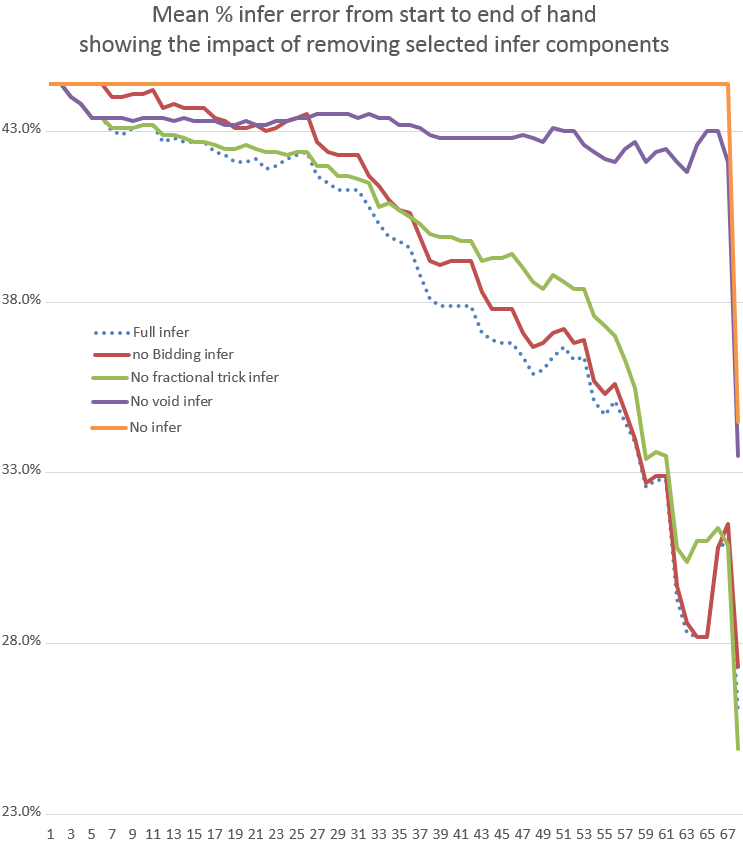
Figure 7 Plot of mean error per card during hand for 10 hands
Note that at the start of game, after the deal, all card projections are 33% (rounded) as each player knows that cards they do not have must be held by one of the other 3 players, so the chance that each will hold this card is 33%. Net this totals 100%. We can assess the average error of any estimation by taking the actual card situation, which is either 0% or 100% and differencing this with the estimate. If you take the mean of these at the start of game it comes to 44.4%.
That throws up a slight paradox. If instead the probability estimates were instead all set to 0%, then the average error would be 33%, i.e. less. However we have to work on the basis that these figures are meaningful to allow projections of deals, so we have to peg at this apparent higher error rate.
Taking the 10 game average (mean of 40 values per point) above we then see the drift in inference accuracy, predictably reducing the error as the hand progresses. Note that this does not include the probability value of the cards that each player actually holds and therefore knows about, nor does it include any card exposed in play.
If we look at the values plotted:
| 1. | Full infer (blue dotted) | |
| This starts at 44.4% and drops to 26%. This uses all inference components | ||
| 2. | No Infer (orange) | |
| This predictably only changes with the last couple of cards, when a rare exact absolute inference can be made. | ||
| 3. | No fractional trick infer (green) | |
| This is the main subject of this article and it can be seen for the first 40% of the hand that this has limited impact, only marginally worse than full infer. However in the following 40% of the hand this widens to nearly 3%, tailing off as the hand completes. | ||
| 4. | No void infer (purple) | |
| Predictably this has a massive impact and losing void inference badly damages the accuracy of inferences overall. This leaves the overall accuracy near to "(2) no inference" | ||
| 5. | No bidding inference (red) | |
| This clearly has an immediate impact on accuracy, as would be expected, but rapidly tails off, shrinking to no impact. This balances coverage with "(3) No fractional trick infer", providing information at the start, while the latter takes over later in the hand. | ||
Does this inferences system significantly impact performance? Was it worth it?
First the simpler inference of voided suits is already huge and inevitably will have the most dramatic impact, but here we are instead assessing the cumulative impact of many imprecise inferences. The actual values used to make these changes are not mathematically derived but rule-of-thumb estimates. They are ripe for tuning, but the values primed are plausible.
Running block tests head-to-head between a version that uses full inference and one that only uses absolute inferences such as voiding suits, shows an improved rate of winning points by 15.4%. This is very significant, as the impact of hand quality has a substantial random smoothing impact on play success. It might well be the case that a perfect player might only win points some 25% faster than this player. The latter figure is conjecture but makes the point that luck also has a significant impact on play success.
Looking further we tested full inference against a version that uses absolute inferences such as voiding suits, leaving all cards with exactly the same probability. i.e. 33 33 33 becomes 33 33 00 not 50 50 00. This then mimics a flat probability system. The result of this was essentially the same as above, so these small skews caused by values of 33% and 50% to both, appear to not significantly change the result.
Net this inference system is crucial for the program to play well. Without it many test deals will clearly not reflect the game situation and inevitably lead to inferior play.
Jeff Rollason - January 2019
