Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
The previous article "Reducing the burden of knowledge: Simulation-based methods in imperfect information games" explored the mechanics of how to represent MCTS (Monte Carlo Tree Search) trees with imperfect information using ISMCTS. This article takes a measured step back and re-reviews the whole idea of searching with imperfect information and re-explains what this is, and then considers how it can be best managed.
A core object of this article is to give the reader a more solid grasp of the essential nature of imperfect information search and how it differs from perfect information search.
Searching in Games
Historically using search to solve games has primarily centred around perfect information games, such as Chess, where the domain being analysed was completely explicit. The obvious primary paradigm for this was minimax, but in recent times MCTS has proved effective within the same domain, even in extremely difficult games such as Go.
Minimax here generally searches a series of iteratively deepening searches, each depth first, stepping serially through the search tree moves. Each iteration is essentially an indivisible step, each of which may require the exploration of hundreds of thousands of moves before any result can be obtained. Each iteration takes geometrically more time, so the method becomes inflexible when attempting to extend the AI think time.
In contrast MCTS with perfect information has the exploration of a single node as the indivisible step, so that MCTS can be stopped any time to reveal a "best" move. Also MCTS can explore the tree in any order, unlike the serial scan of minimax.
Examining Perfect Information Search Behaviour
Lets have a look at what minimax and MCTS perfect information trees might look like:
Minimax in its simplest form attempts to completely explore the entire possible search space to a fixed depth, but optimised by alpha beta to only look at variations it absolutely needs to determine the optimum move choice. A chess search might reveal an exact answer such as "If I play X, I mate in 4 moves".
In practice minimax search implementation is somewhat more complex than this and in practice branches somewhat vary in depth as different criteria are used to drive different parts of the search. Also there are a multitude of ways to apply non-exact optimisation to massively reduce the search space without undermining the search conclusion.
Diagrammatically a highly simplified version of such a search might look like this:
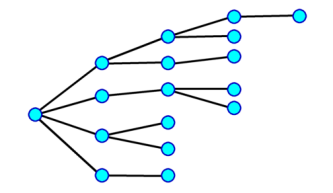
The key point here is that the search is not limited to the iteration depth. Some variations may expand to substantially greater depth. So each iterated search will on average search deeper.
If we look at MCTS in this context, a key difference is that MCTS generally avoids expensive complex evaluation so that more positions can be considered. This generally looks at the entire depth to end of game so that evaluation is reduced to the simple question "Did we win?". Even if the end term is more than win/lose and based on some evaluation, this value is not literally passed back to the root to deliver a value, but instead used to modify the entire branch from root to leaf. The value impacts what is looked at next, not any absolute evaluation for comparison with the root. This is a key difference between Minimax and MCTS.
Unlike minimax the choice of move can select any tree node to expand, randomly skewed to look at moves that previously showed a better chance of leading to a win.
Such a search might look like this:
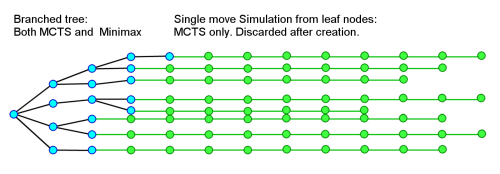
This may seem very different to minimax as the tree goes all the way to conclusion. However if you observe the actual behaviour of the backup system it looks quite a lot like minimax, but making gradual shifts in move choices within the tree rather than the instant brutal cut-offs that minimax executes.
Summarising this, and additional points, the differences for perfect information are:
Minimax variable depth, iterative deepening:
- Iterations are indivisible. Moves are delivered after iteration completion. Iteration cost geometrically increases, eventually impeding the option for "lets think just a little longer".
- Intra tree move selection is very limited. You can only pick moves from within the current move list. You cannot jump to another part of the tree.
- Evaluation values are passed directly back down the tree. The evaluation is very closely tied to the eventual move choice.
- Tree is not held in memory, only the current branch and moves list for each branch.
- Good for calculating exact questions such as "is there a mate in 4?", which it can be answered exactly.
MCTS
- Unlike Minimax the indivisible unit is now a single node. It can be stopped at any time. The tree can be searched in any order.
- No literal evaluation passed back to the root. Values are used to just control what gets searched next, not what is to be played. Move choice is from the basis of "most searched", not "highest evaluation".
- The tree is held in memory, grown as the search progresses. The single strand simulations or rollouts however are discarded after creation, simply to return a single value.
- No guarantee that any exact best move can be found, so not ideal for proving "is there mate in 4?"
Despite these differences, both will share the idea of a primary continuation and MCTS actually converges to a minimax solution.
Jumping to MCTS with Imperfect Information
We are now moving to consider MCTS with imperfect information, revealing now 3 categories of search:
- Minimax with perfect information
- MCTS with perfect information
- MCTS with imperfect information
Problems
First, how can you search when you do not know what is going on?
This is a blunt but valid question. In the case of a trick-taking game, such as Bridge or Spades, we simply do not know who has what card, so how can we meaningfully search this space?
If we are going to search we will have to "guess" who might have which card. Our guess can at least account for knowledge we do have, such as "Player X is void in Suit Y", from simply observing play. We can refine that with other non-exact play inferences, such as "a play trying to win zero tricks is unlikely to have many master cards".
Given this we could guess once and hope our guess was right, but obviously this would be an improbable plan as our single guess will inevitably be very poor indeed.
Note also that this search of a guessed deal assumes that we search against an exact set of cards, so we are viewing all cards at all times. This is analysing as if we were cheating. A flaw in this is that it would not be capable of generating anything akin to a "probing" play (e.g. play a club just to test if X has any clubs). Such a strategic play would have no meaning if we can see all cards.
So we are going to have to somehow guess a number of times and search each of these guesses separately.
Search 4 deal guesses?
This is a step in the right direction. Evidently if we could process a vast number of deal guesses, and search all of these, then this intuitively must deliver the prospect of being able to make a better "average choice".
If we search 4 trees:
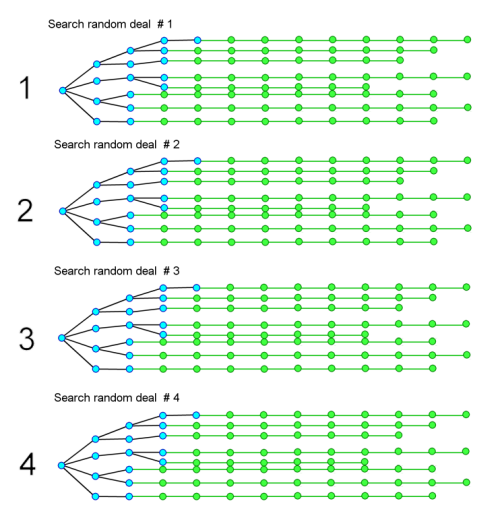
We could complete this and then sum the number of searches for each move for each of the 4 deals and make a move selection from that.
However this is still only 4 deals and so is a weak projection of what the opponent may have. A statistical sample of 4 is pretty weak.
On top of that we have had to complete 4 searches instead of one, so our cost will have increased. We would be obliged to speed our searches up.
It is reasonable to suppose that we will need to search many more than 4 randomised deals, but the likely cost of this will increase dramatically, so it is not looking very practical.
As an aside, a variant on this has been tried for Bridge, but using multiple randomised deals, searched using a highly optimised minimax search. This depended on a great deal of domain specific knowledge for Bridge. The program played well, but still needed a significant processor resource.
Lets try something very different: ISMCTS
(Information Set Monte Carlo Tree search)
Having dished the alternatives we could consider a search that created a large number of randomised deals, but that all shared the search results of these, all inside one search tree.
The obvious logical flaw in this is that surely the play paths in one deal will not be legal for another deal, so that very few move sequences in the search will be legal in the actual hand being played.
From that it sounds like this is a nonsense idea. However if we step back then we could imagine that we are creating a tree for any eventuality. It will inevitably have many more branches as after any one card is played then the range of possible cards that might be played, across a large number of random deals, could be immense.
This is still an uncomfortable idea as inevitably the tree cannot contain all the variations of all the deals that would have arisen from searching each of these randomised deals. In addition to that a common legal move sequence from two deals might draw a radically different conclusion because of the cards available at the end of the sequence. Therefore logically they cannot share the same returned value.
Then comes the next shock: We only create a single rollout per randomised deal. So each deal only has one unique branch, at most. So there is no intra-deal minimaxing of a move choice.
This takes us further out of the comfort zone of our imagination as this is now far removed from any human method of analysing a game position.
Lets take a look at this from a practical example from the game of Spades, a 4 player partnered trick-taking game. We will be analysing for the first card played from 52 cards to be played until end-of-hand.
Examining actual ISMCTS trees
Lets look at a real example of ISMCTS working, but first unleashed on a fixed deal so that each time it is presented with the actual cards being played (or some randomised deal but duplicated for each search). This turns it into a perfect information search. In doing so we can see something close to a regular MCTS perfect information search.
In the diagram above we are shown an average branch in this tree, with most branches having around 3 legal plays, with every 4th node having more corresponding to the first card in the trick, where the player has more options.
From this we can see that the peak number of leaf nodes searched is at ply/move 8, or the 8th card played. Note that the tree ends at ply/move 15, after which we only have single thread simulation rollouts.
Note that ending at move 15 means that the single thread simulation rollout proceeds all the rest of the way to the 52nd card of the hand. That means the tree covers only 30% of the entire depth. The remaining 70% will be a generally poor move sequence, almost all of which will never ever be an optimum sequence.
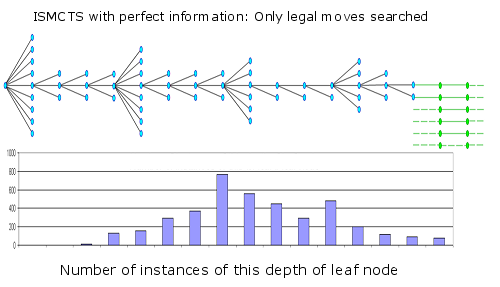
Lets compare this to an actual ISMCTS search with imperfect information from the same position analysed.
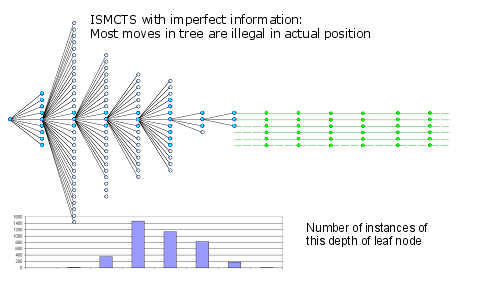
Here the nodes that are legal in the actual position are shown in blue and illegal nodes in white.
The most obvious dramatic change here is that the tree is both much wider and shallower. The most common leaf node is at ply/move 4, instead of ply/move 8. Since the nodes shown here are for the average branch we can see that for the early branches that most nodes are illegal.
We can project this calculation and discover that only 1 on 6000 leaf nodes are legal in the actual position being played.
Also note that the maximum depth is 7, so 7/52 = 13% of the entire sequence is inside the tree with 83% being the single thread low quality simulation. Of this 13% full tree depth there will be almost no legal variations in the actual position.
This looks like an ominous conclusion. From this observation you might reasonably conclude that this was already an automatic failure.
However the basis of that judgement rests on the expectation for the need for concrete variations, which is the essential basis of perfect information search. This needs a change in mindset. What ISMCTS delivers is a much more fuzzy statistical estimation of success. The basis of each rollout is actually very weak indeed, depending on a very flaky continuation. However the follow-on variation from an inferior move will also be flaky, but just a bit more flaky.
The point here is that we need only a relative measure of quality. In minimax and MCTS with perfect information we are comparing the best line from X with the best line from Y.
In ISMCTS we are comparing a poor line from X with a poor line from Y. After a large number of trials X will deliver a better result than Y, if X is actually better than Y. It will have done that without ever looking at anything close to an optimum variation.
Performance
We need to see if this actually works, so need to look at some results. The following shows the performance of our Spades program as it progressed from a static probability evaluation to a mature ISMCTS program.
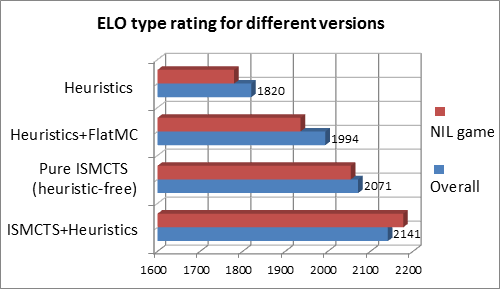
In the above chart the first version of the program played using a static probability function that played moves with no search. This was quite sophisticated but was vulnerable to incorrect evaluation of trick-play combinations.
The second embedded the above inside a simple Monte Carlo rollout, with no tree search. This delivered a credible advance in play quality as it plugged some of the holes where the heuristic-only version would make mistakes.
The third version above used ISMCTS, but here all evaluation is switched off. Despite this it out-performs the heuristic-rich monte carlo version. This is more of an academic exercise than a practical proposition, but makes a point: Even with no knowledge you can deliver credible results.
The final version uses ISMCTS combined with some heuristic input, which finally lifts the program to a strong credible performance. This will be described in a future article.
However there are no free lunches. It should be noted that version 3 above out-performed version 2, but actually was perceived as weaker. The issue is a core problem of MCTS as a whole. Given two moves that both either lead to a very likely win or loss, MCTS could randomly choose either. This might mean playing a completely absurd card that still leads to an inevitable win. This is not practical for human opponents. A program not only should play well but be perceived to play well, otherwise people simply will not play it. To put that in a human context: would you want to play against someone who, when they know they will win, will simply close their eyes and thereafter play random cards from their hand?
Conclusion
ISMCTS represents one of a number of forward-thinking methods of analysis that sits outside our immediate experience. I.e. we could not exercise such a method to control some activity in our life, but it does deliver a meaningful result in a domain where intuitive methods do not really fit. Another such method is the Bonanza method of optimising 10 million learned parameters to deliver an evaluation in Shogi, whose conclusions are statistical rather than analytical. These methods are outside our common experience.
As time progresses, more such effective methods will be discovered that take us outside our capacity to intuitively understand them, but will deliver more and more real and capable methods of achieving real results. ISMCTS is certainly one of them.
Jeff Rollason - March 2014
