Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
A previous article, Mixing MCTS with Conventional Static Evaluation, talked about how we had applied MCTS to combine with our Spades static evaluation to create a stronger program. This article looks at the methods we used to make Spades stronger still. An issue here is that Spades has elements in the game that are hard for a static evaluation to handle, but the engine has evaluation at the core so we needed to evolve this core to manage the needs of stronger play.
This article also has some key reflections on the issues of using UCT-based MCTS with games such as Spades.
The Background
Note first that the Spades game engine was based on a static evaluation that used probability to determine the possible outcome of playing any one card. It worked by first assessing the goal at any one stage ("are we short of tricks given the cards remaining?") and then assessing the likelihood that playing any one card would contribute to achieving the desired goal. This needed to have an idea of the chance that the opponent would be able to take the current trick. Part of this is having an idea of the probability that your opponent possesses each card, and also needed to take into account additional goals, such as voiding in suits or stopping an opponent taking a trick. The desirability of each of these goals was assessed and combined with the likelihood of success, and these combined into a linear evaluation used to select a move.
How successful was this?
The above method, after iterated development by observing play, resulted in a game engine that appeared to play plausibly well. However a huge defect was that in certain points in the game it could play quite badly. In particular the last few cards where, for a human player who can count cards, the play is pretty simple, the game engine would play some very bad plays. Added to this the sub part of the game is Nil bid play, which the evaluation played very weakly as the goals of this are hard to evaluate. In Nil bid play you need to make your tricks while trying to give tricks to your Nil bid opponent.
How successful was the conversion to MCTS?
This was apparently very successful on first trial as MCTS was winning easily against just the evaluation-based game. However this was an illusion. What MCTS brought to the table was the capacity to have a plausible shot at most parts of the game, whereas the evaluation-based version just critically played some parts very badly. In terms of winning points this left MCTS well ahead, but most moves were actually worse. The evaluation-based version played plausible moves most of the time, but was crippled by key very bad plays. These rarer very bad moves multiplied the probability that a move based on MCTS would include such a move, such that a very high proportion of all moves assessed would depend on at least one of these bad moves, compared to evaluation-based assessment which restricted the influence of these bad moves to a small subset of all moves.
This first version required an overhaul of the evaluation to remove as many major weaknesses as possible. This still had limited success with the Nil-bid part of the game, but at least delivered reasonable play.
Preparing for the new version of Spades
Our Spades engine is highly rated but still attracts criticism about Nil-bid play and also over-concentration on bagging. We very clearly needed to step up the engine to the next level. Plan A was to again return to improving the evaluation by adding terms to the evaluation to deal with aspects of play that it currently handled badly. This further increased the complexity of the evaluation, with many conditional branches and 94 distinct evaluation terms.
Next task: Tune the existing evaluation
This is the point where tuning the existing terms was the next needed step to get good values for each of the 94 terms. Up until this point the values of these terms started with some balance, but after the plethora of added terms the job of balancing these by hand quickly becomes impossible. With 94 terms, each with an attached value, it becomes increasingly impossible to imagine that the evaluation could be anywhere near optimum.
Hand tuning here feels akin to blundering blindfold through an invisible huge multi-dimensional evaluation space. I guess if it is invisible, then you do not need a blindfold, but somehow the metaphor feels appropriate.
Tuning strategies
The most obvious method, and not without some success, is to simply play through games, spot errors and tweak terms to get better results. The evaluation for Spades has lots of nice colour diagnostic messages explaining the terms, so that it is easy to spot why some inferior move has been made and then either make an adjustment to an existing term, or add some new term to fill in missing knowledge.
This process allows the user to see a bad move, correct it and check the result. Superficially the repetition of this method should result in a gradual improved play. However, as detailed in the joint article in this newsletter, Evaluation options - Overview of methods, this does not guarantee good progress.
The impediments to progress here are what must be inevitable holes in the evaluation that the developer does not spot. Some of these can be spotted by endlessly playing games and looking for aberrant play, but this is potentially very hard work. Also, critically, it may systematically fail to expose a whole range of medium sized defects, which on their own are not enough to create very bad plays.
Biting the bullet: Automated tuning
Having embarked on a period of manual "tweak-and-test", it was clear that the actual tuning of all the 94 parameters as a whole needed to be addressed, so the program was prepared for such tuning. This required a long period of careful embedding of floating point parameters into each of the evaluation terms, so that they could be tested. The next step is to establish a methodology to tune these, as follows:
Stage 1: Create a training set
A real spades database is maybe just not available, or hard to create and then also inconvenient to reference by the program. A plausible approach is to create a record of an automated game, played at a high level, and compare each of these higher level plays (created by a combination of evaluation and MCTS) with the moves that the simple evaluation would have created. This is slightly incestuous as this record must share some of the defects of the evaluation used to create it, but such a process can be iterated with improved training sets.
Stage 2: Try serially tuning each parameter one-by-one
This will tune parameter 1 to find the sweet spot, then 2 etc.. Once it reaches the end, it can repeat with parameter 1, looping until they are all stable. This setup really is used to test the validity of the mechanism rather than hope that it could yield a meaningful result. A fundamental issue is that many parameters will be part of a critical subset, which requires one parameter to be modified in conjunction with another. Tuning just one parameter might be doomed as it just cannot be meaningfully modified in isolation. Another issue is that an early parameter might grotesquely distort its value to avoid some evaluation issue because of a later parameter. It then may be set to a value that is very poor across all other possible sets of combinations and thereby doom the tuning to sit at the top of a very poor hill in the evaluation landscape.
To visualise this I have borrowed an image from the earlier article The Computer learns to Play Poker:
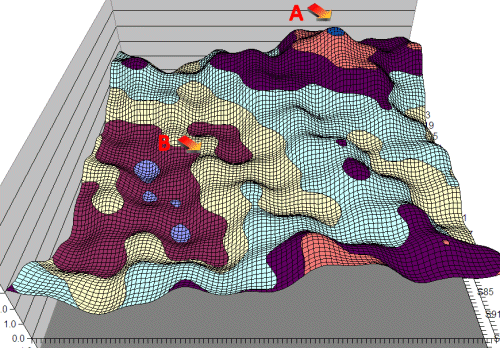
In this scenario we may get locked at B with no tuning path to reach A, as all positions close to our evaluation point are inferior to the current position.
Stage 3: Try serially tuning each parameter one-by-one, but with scaling
This is an optimistic variant of "2" that causes each re-tuned parameter to only slightly shift in the direction of an optimum point before going on to the next parameter, so "graduated". I.e. parameter 1 may return a re-optimised value of 0.18x (starting from base 1.0x), but that it would record some shift in that direction rather than the literal value. So it might be recorded as 0.95x during the first pass. On the second pass it has a chance to make a similar shift in the same direction until it eventually finds "rest". This is better than "2" as it allows later parameters to shift before the initial parameter has fixed some wayward point. Of course this assumes that each parameter may have some bell-like shape, so that we do not get trapped inside just one multi-hill evaluation tune step. This scheme appears to be a plausible approximation to changing all parameters in parallel, and would generally look like a reasonably plausible strategy to try.
Stage 4: Iterated random changes across a block of parameters
This modifies all or a group of parameters in parallel, adopting any improvements and repeating the process. In practice modifying all parameters at once is maybe inviting no progress, so best to modify a subset at any one time. If that is a random subset it will naturally eventually find the set of changes that improve the overall net score. Note that this is not simply a simple random change, but random on a log scale, so that you have a uniform distribution of both tiny and huge changes. Without this all changes between 9x and 10x will be much more common than all changes between 1.1x and 1.2x, which would not make sense.
Stage 5: Renewed training sets
Having made progress with methods above, you then need to create a new training set and repeat the progress.
Is this good?
At first glance this looks a bit win-win as surely this system can only have benefits? However it sadly has the capacity to make things fundamentally worse. The issue is that our evaluation, with 94 terms, stands a very good chance that it actually needs more terms. Because it was hand-tailored each term may still have a plausible initial value. However, after learning, the parameters may get tuned to compensate for some other missing defect. To give a Chess evaluation metaphor, if the evaluation cannot handle protecting kingside pawns, it may tune to stop castling altogether. This is avoiding the problem that needs fixing. So the tuned version now hides the situation that needs to be fixed, so the defect has been "concreted-over". With Chess this issue may not be so serious as the absence of castling is such an obvious defect, so the need for a fix might not be hard to spot. It is not a given though as, although the defect is recognised, the reason for the defect may not. In Spades this potential obscurity is likely to be harder to solve.
How did these systems perform?
Looking at the methods above, it is not obvious how they would perform. Part of the issue is that the evaluation is largely an invisible 94-dimensional space whose actual shape is hard to imagine. In consequence prediction of the behaviour of the above depends on somewhat limited reasoning rather than meaningful knowledge.
Anyway, we can compare these to reveal the properties of each. These results below are limited to the first 47 parameters, concerning with the simpler non-Nil part of the game. The results were as follows:
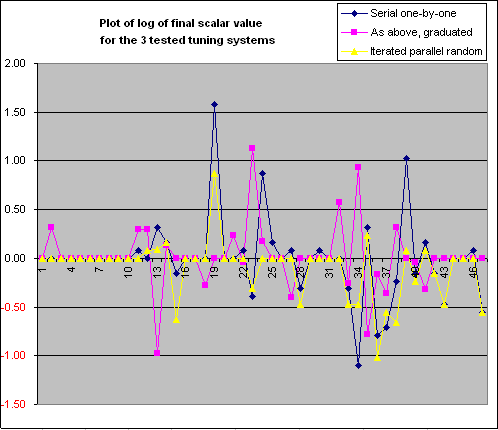
These results spell it out in black and white that indeed even the 47-dimensional sub-space must be very "lumpy" indeed. Optimistically we might have imagined that each of these methods might each be a limited approximation of the other, implying a kind of hill climb towards some general maximum common peak, but where each method reached a different sub-optimum point.
That clearly did not happen as each plot seems to scarcely bear much relation to each other. There is some commonality in that parameters 4 to 9 showed no value, but the rest looks largely pretty well random. The largest offset parameter 19 is both highest for the blue and yellow plot, but unaltered for magenta (which should have been more credible than the blue plot).
Applying "reason" it would seem reasonable to expect that only graduated serial (3) or iterated parallel random (4) would offer any credible tuning. However the basis for choosing between these is a bit flimsy. "Graduated serial" assumes that we are already on some upward evaluation slope and that we just need to determine the exact direction to head in this 47-dimensional space. "Iterated parallel random" allows us to jump to nearby spots in the evaluation space, which might not be reachable by "graduated serial" above.
Which was best?
The only meaningful means of assessing these tuned parameter sets is to try them out in play testing. The original and tuned sets were played in auto-tests against the original evaluation and, from this, both serial versions were actually weaker. However the iterated random showed an 80% increase in the accumulation of points so, after further iterations, was used as a basis for the new version.
This new version will be released in October 2012.
UCT and Spades?
Between starting this article and completing, I attended the "Workshop on Games at the University of Essex", and this offered a chance to look again at UCT. UCT is an enhancement of MCTS that tracks the success of explored nodes in the rollout, so that successful branches are re-visited more often. This very simple idea transforms MCTS to become a remarkably powerful AI method.
Given the sometimes overwhelming issues in creating a complex evaluation, UCT-based MCTS offers a system that can work without heuristics/evaluation. A UCT-based program can have rules added to the game and will automatically adapt, unlike a heuristic-based program which necessitates handcrafting the evaluation for each new added rule.
However UCT, although ideal for many perfect information games, has issues with imperfect information. Some successful research into such games has migrated to some unnatural looking solutions. For example basing a move choice on many determinisations (randomised projected game situations, assigning pseudo-random choices to hidden information) and then searching each as if each were a perfect information game. The result of all of these separate searches is combined to select a move. The defence of this method is that "it works". Note though that the return for UCT polling is then inevitably less efficient than a UCT search of a perfect information game as you have to discard state information between each determinisation.
However I can sense the uncomfortable wriggle in their seat when the question is raised as to whether or not there is any theoretically sound basis for this. It appears to work by solving problem A that then works as a solution for problem B. In practice it might be that this approach will work with a whole raft of imperfect information games but, in varying degrees, there will likely be many games where it does not work well and even some where it works badly.
One evolution of this is to find a common set of shared search information that can be shared by multiple searches, where you are not recording exact states but move sequences, much like primary continuations as used in chess. This is a line being followed.
However, stepping back, these tweaks may in the short term deliver varying degrees of successful play but the legitimacy of them still feels a tad suspect. As soon as you have the results of the very first rollout, the progress at that point already violates the basis of hidden information. You are then already, in a sense, "cheating", although you are cheating against randomised rather than real opponent data. You are solving an imperfect information game by combining the results of multiple perfect information analyses. This may "work", but it is an uneasy solution.
Perhaps imperfect information games cannot be so effectively or easily solved as perfect information games using UCT, but instead these more obscure tangential UCT approaches will need to be used. The rewards for succeeding are great, so the pursuit is certainly very worthwhile. UCT promised to deliver intelligent systems across a very broad range of applications, inside and outside gaming.
The ultimate test will be if such techniques can play imperfect information games where the theoretically best play is a "probing play" (e.g. play a club to test if your opponent is out of clubs). The above methods appear that they might not to be able to easily deliver this, so this type of example may prove to be the ultimate litmus test for UCT for such games.
Jeff Rollason - September 2012
