Department of Data Science and Knowledge Engineering, Maastricht University
Copyright Notice: This article is Copyright Mark Winands. Ideas and code belonging to Mark Winands may only be used with the direct written permission of Mark Winands.
In recent years a new paradigm for game-tree search has emerged, so-called Monte-Carlo Tree Search (MCTS) [1] [2]. In the last ten years it has achieved noticeable success in a wide range of domains such as puzzles, card and board games [3]. It is final breakthrough to a wider AI audience came through its contribution to the astonishing results of Alpha (Go) Zero, which established supremacy not only in Go, but also in Chess and Shogi [4] [5].
In this article I will give a background and a brief overview of the technique. I am not claiming that this article covers every aspect, and be warned it is coloured by my own experiences.
How it Started
For decades minimax search techniques such as alpha-beta, expectimax or paranoid search have been the standard approach used by programs for playing board games such as chess, checkers, backgammon (and many others). Over the years many search enhancements have been proposed for this minimax framework to further enhance its effectiveness. The victories of Chinook and Deep Blue in Checkers and Chess in the nineties further sealed its reputation. Still many handbooks of AI will explain the minimax framework as a starting point for searching in games.
In the late 1990s research in Chess started the wane off, causing an increasing shift in another well-known board game took place. This was the ancient and popular board game of Go, where the traditional minimax approach was not successful. Not only had the large branching factor prevented a deep lookahead, worse the intricacies of the game hindered the construction of an effective board evaluation function. Go is full of relatively vague concepts such as life-and-death, territory, influence, and patterns. This implicit human knowledge is hard turn explicit in a static board evaluator. Without such an evaluation function alpha-beta would fail. The Go community was desperate in those days. It started to look to alternative AI techniques such as decision trees, rule-based approaches, theorem provers, and pattern recognition. Basically one did not had to buy AI handbook to get an overview of the AI field, simply reading the computer Go literature would introduce one to most of the AI techniques available then.
When I entered the games research scene in 2000, I participated with my Lines-of-Action (LOA) engine in the ICGA Computer Olympiad. Besides operating my own engine, in the breaks I watched also the entries in the other games. While in games such as Chess and Awari the level of play was at least grand-master level, in the Go competition the machines did not reach even a proper amateur level. Go was the tournament where spectators came to have a good laugh. A strong amateur player could defeat a Go engine with a 20 to 30 stones handicap. The ICGA even started to reintroduce the 9×9 tournament at the Olympiad of 2002. This version of the game has a similar branching factor as chess, taking out one of the big hurdles. But even in this variant, no strong play was achieved. The engines still had not had a clue how to play a decent game of Go.

Figure 1: The 2001 Computer Olympiad in Maastricht - where 47 competing programs battled to prove algorithmic supremacy
In 2003 I was a PhD student at Maastricht University, doing mostly research in the game LOA, where I was investigating proof-number search among others. The headquarters of the ICGA were in the same place in those days, and so was the coordination of the Computer Olympiads. And so I got involved organizing the 2003 Computer Olympiad in Graz. One of my jobs was also arranging hardware for the participants, as laptops were not that powerful and remote computing was not allowed. Bruno Bouzy approached me for asking a strong machine as he was using Monte-Carlo evaluations in his engine INDIGO. I was somewhat surprised as usual Go engines did not rely on computing power too much, as search did not really help. What was happening?
The idea was replacing an evaluation function with Monte-Carlo sampling for dynamically evaluating the merits of a leaf node. At such node a number of games are simulated by selecting (semi-)random moves until the end where they are subsequently scored. The average results of these games are then used to assess the position (e.g. Figure 2).
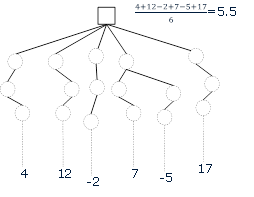
Figure 2: Monte-Carlo Evaluation
This concept was not new, it was originally proposed by Abramson in 1990 [5], who experimented with these so-called Monte-Carlo evaluations in the games of Tic-tac-toe, Othello, and Chess. In 1993 Bernd Brügmann was the first to use Monte-Carlo evaluations in his 9×9 Go program GOBBLE. Success was rather limited as the hardware in those days could not support many simulations, resulting in a flat Monte-Carlo search not able to look not more than one step further ahead. At the moment tactics starts playing a role in a game, such an approach would easily start misjudging positions. An example is given Figure 3, where a flat Monte-Carlo search would prefer node B over node A, as node B has a better average score. However, looking one step further ahead, the opponent has a response to ruin the position in the end.
Still, the following years the technique had more success in games with uncertainty, where the added value of search is more limited. It was incorporated in stochastic games such as Backgammon [7] and imperfect-information games such as Bridge [8], Poker [9], and Scrabble [10]. It was no surprise that sooner or later the idea would pop again at the moment hardware would have advanced such that more simulations per second could be executed. It was Bernard Helmstetter who saw the potential and convinced Bruno Bouzy to look into it. Together they presented their approach [11] at the well-established Advances in Computer Games conference, which was co-hosted with the Computer Olympiad in 2003. It was not the breakthrough as their programs OLEG and INDIGO did not had the success as they hoped for at the Computer Olympiad. Worse it was ridiculed by some in the community, as the saying was with Monte-Carlo evaluations you are averaging, and the final tournament will also be average.
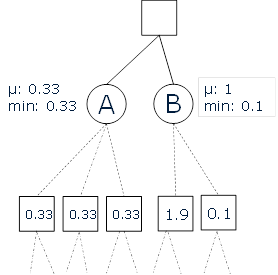
Figure 3: Flat Monte Carlo
The Dawn of MCTS
Still Bruno Bouzy strongly believed and continued trying to find ways to effectively combine Monte-Carlo evaluations with game-tree search. In 2004 his engine INDIGO was able to get a bronze medal at the Computer Olympiad, held in Israel. Especially noticeable was that it outperformed GNU GO, which was the benchmark engine at that time. This result started to attract somewhat more interest in the approach, and one of the research domains was the game of Clobber.
In 2005 the Olympiad was in Taiwan, and as I had never been there, I decided to write an engine for Clobber, a combinatorial board game for which it is hard to design an evaluation function. I went for the classic alpha-beta search with a rather weak evaluation, whereas Jan Willemson competed with his Monte-Carlo engine CLOBBERA. His engine got a beating by mine (8-0).

Figure 4: Mark Winands with Jan Willemson, medal ceremony Clobber tournament
Monte-Carlo for Clobber would have probably died there, if the games would not have been watched by Levente Kocsis. I had co-authored a paper with him at the associated games conference, so he was interested how my engine was doing. After the games all of us started to hang out with each other. At one night, after a few drinks and going back to our rooms, they started to discuss Jan's Clobber engine, where Levente mentioned that there were interesting developments to try out. There they started to make plans to collaborate, and without realising it, I witnessed the birth of MCTS. A few months later Jan asked me if I could send them my Clobber engine in order to use it for benchmarking their Monte-Carlo engine using an idea called UCB. In hindsight in these months the MCTS variant UCT was being conceived!

Figure 5: Panorama of tournament (Remi sitting left of middle)
MCTS Arrives
Many people over the years have claimed that they have invented MCTS. And yes, combining search and Monte-Carlo had been tried earlier, even using ideas from the multi-armed bandit problem area. Frankly, it was Coulom to put MCTS on the map by presenting the idea at the 2006 Computer and Games Conference [1]. He subsequently demonstrated its strength by winning the 9×9 Go tournament at the 12th ICGA Computer Olympiad with his MCTS engine CRAZY STONE. The key insight was applying as a best-first search method that by using the results of previous explorations, gradually builds up a game tree in memory, and successively becomes better at accurately estimating the values of the most promising moves. MCTS consists of four strategic steps, repeated as long as there is time left [12] [13]. The steps, outlined in Figure 5 are as follows. (1) In the selection step the tree is traversed from the root node downwards until a state is chosen, which has not been stored in the tree yet. (2) Next, in the play-out step moves are chosen in self-play until the end of the game is reached. (3) Subsequently, in the expansion step one or more states encountered along its play-out are added to the tree. (4) Finally, in the backpropagation step, the game result is propagated back along the previously traversed path up to the root node, where node statistics are updated accordingly.
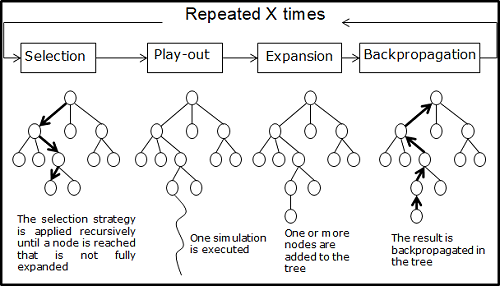
Figure 6: MCTS Scheme
So what about that MCTS variant UCT? Well, it was implemented in Willemson's Clobber engine that competed in Clobber tournament of the 2006 Computer Olympiad at same time Coulom competed in the Go tournament. The main difference with Coulom's approach was that it used the multi-armed bandit algorithm Upper Confidence Bounds [14] applied to Trees (UCT). In the selection step a child k of the node p is chosen according:
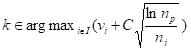
where vi is the value of the node i (average reward), ni is the visit count of i, and np is the visit count of p. C is a coefficient (e.g., 0.2-0.8). This mechanism balances exploitation and exploration, i.e. investing time in promising lines, but still putting some effort in the apparently less promising in order to prevent overlooking a strong one in the long run.
Unfortunately, Willemson's Clobber program did not do well, and UCT would have been forgotten. But fortunately, Coulom tried the UCT mechanism a few weeks later in his Go engine, and reported the improved results on the Go mailing list. UCT became the way to go. Though the work cited would be the application of UCT on the sailing planning problem [2] and not the Clobber work [15].
MCTS Matures
Afterwards, MCTS enhancements for the UCT mechanism such as RAVE, Prior Knowledge, Progressive Bias, and Progressive Widening [12] [16] have made MCTS effective in many challenging domains with a relatively large branch factor (such as 19×19 Go). Another boost that MCTS got is that nowadays desktop machine contains several cores, making parallelization [17] feasible. MCTS is relatively easy to parallelize, simply sharing a search tree with several threads will hardly cause any racing problems, as MCTS is handling noise rather well anyway. The algorithm has shown almost near linear speedup in terms of strength up to 64 threads [18], outperforming alpha-beta search in scalability.
MCTS has become at first the dominant search technique in quite a number of abstract games besides Go, also in Amazons [19], Lines of Action [20], and Hex [21]. At our department, we have applied MCTS successfully in video games such as Ms Pac-Man [22] and the General Video Game AI domain [23] , where our agents have won their respective competition. MCTS has not only showed to advance the playing strength in many domains, but also to increase the entertainment level by playing plausible moves [24]. Moreover, MCTS is finding its way into commercial applications such as SPADES by AI Factory, a mobile game with 6.8m million downloads, PRISMATA by Lunarch Studios [25], or the AAA title TOTAL WAR: ROME II by Sega, a PC game with over 1.13 million copies sold. Furthermore, MCTS is utilized in serious gaming (for games meant to train or educate [26]). Finally, MCTS can also serve as a tool for content generation and game design [27].
However, there is nothing of MCTS specific to games. It is applicable to planning, decision making and optimization in a wide range of domains. This can range from robotics [28] to operations research [29], from logistics and transportation [30] to medical applications [31], from security modelling [32] to space exploration [33]. Applications of MCTS variants include utilizing the frequency spectrum of radios dynamically [34], scheduling patients for elective cardiac surgery [35], and managing the electricity demand of consumer devices [36].
Concluding
Monte-Carlo Tree Search (MCTS) has caused a revolution in AI for games due to its three main selling points. (1) As MCTS already works with little domain knowledge required it is a good candidate if handcrafting an evaluation function is difficult or when rapid prototyping is required. (2) The MCTS framework can be easily modified to be successful in a whole range of games, which may have two or more players, chance or determinism, or being fully or only partial observable. (3) MCTS is relatively easy to parallelize and scales quite will, making it an attractive technique for multi-core machines.
However, for MCTS to work effectively search-control knowledge is required to guide the simulations. Techniques such as RAVE, Progressive Bias, Progressive Widening and others have to be applied in order to get an MCTS agent on expert level for many domains. It is crucial that the play-outs are informative. If possible, applying a static evaluation function or a small alpha-beta search in MCTS can boost its performance even further. It is therefore a myth that classic adversarial techniques will become obsolete. Even if it is not possible for a particular domain to use them directly, enhancements such as static move ordering, history tables, and transposition table can be applied in MCTS in some way or another. Properly understanding ideas from other adversarial search techniques is beneficial for developing a state-of-the-art MCTS game playing agent.
References
[1] R. Coulom, "Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search," in Computers and Games (CG 2006), Springer, 2007, pp. 72-83.
[2] L. Kocsis and C. Szepesvári, "Bandit based Monte-Carlo Planning," in ECML-06, Springer, 2006, pp. 282-293.
[3] C. Browne, E. Powley, D. Whitehouse, S. M. Lucas, P. I. Cowling, P. Rohlfshagen, S. Tavener, D. Perez, S. Samothrakis and S. Colton, "A Survey of Monte-Carlo Tree Search Methods," IEEE Transactions on Computational Intelligence and AI in Games, vol. 4, no. 1, pp. 1-43, 2012.
[4] D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. van den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel and D. Hassabis, "Mastering the game of Go with deep neural networks and tree search," Nature, vol. 529, p. 484-489, 2016.
[5] D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepel, T. Lillicrap, K. Simonyan and D. Hassabis, "Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm," 2017. [Online]. Available: arXiv:1712.01815?.
[6] B. Abramson, "Expected-Outcome: A General Model of Static Evaluation," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 12, nr. 2, pp. 182-193, 1990.
[7] G. Tesauro and G. Galperin, "On-line Policy Improvement using Monte-Carlo Search," in Advances in Neural Information Processing Systems, 1997.
[8] M. Ginsberg, "GIB: Steps Toward an Expert-Level Bridge-Playing Program," in Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence, 1999.
[9] D. Billings, L. Peña, J. Schaeffer and D. Szafron, "Using Probabilistic Knowledge and Simulation to Play Poker," in Proceedings of the Sixteenth National Conference on Artificial Intelligence and Eleventh Conference on Innovative Applications of Artificial Intelligence, 1999.
[10] B. Sheppard, "World-Championship-Caliber Scrabble," Artificial Intelligence, vol. 134, nr. 1-2, pp. 241-275, 2002.
[11] B. Bouzy and B. Helmstetter, "Monte-Carlo Go Developments," Advances in Computer Games 10: Many Games, Many Challenges, 2004, pp. 159-174.
[12] G. M. J.-B. Chaslot, M. H. M. Winands, H. J. van den Herik, J. W. H. M. Uiterwijk and B. Bouzy, "Progressive Strategies for Monte-Carlo Tree Search," New Mathematics and Natural Computation, vol. 4, no. 3, pp. 343-357, 2008.
[13] M. H. M. Winands, "Monte-Carlo Tree Search in Board Games," in Handbook of Digital Games and Entertainment Technologies., Singapore, Springer, 2017, pp. 47-76.
[14] P. Auer, N. Cesa-Bianchi and P. Fischer, "Finite-Time Analysis of the Multi-Armed Bandit Problem," Machine Learning, vol. 47, no. 2-3, p. 235-256, 2002.
[15] L. Kocsis, C. Szepesvári and J. Willemson, "Improved Monte-Carlo Search," 2006. [Online]. Available: http://old.sztaki.hu/~szcsaba/papers/cg06-ext.pdf.
[16] S. Gelly, L. Kocsis, M. Schoenauer, M. Sebag, D. Silver, C. Szepesvári and O. Teytaud, "The Grand Challenge of Computer Go: Monte Carlo Tree Search and Extensions," Communications of the ACM, vol. 55, no. 3, pp. 106-113, 2012.
[17] G. M. J. B. Chaslot, M. H. M. Winands and H. J. van den Herik, "Parallel Monte-Carlo Tree Search," in Computers and Games (CG 2008), Springer, 2008, pp. 60-71.
[18] R. B. Segal, "On the Scalability of Parallel UCT," in Computers and Games (CG 2010), Springer, 2011 , pp. 36-47.
[19] R. Lorentz, "Amazons Discover Monte-Carlo," in Computers and Games (CG 2008), Springer, 2008, pp. 13-24.
[20] M. H. M. Winands, Y. Björnsson and J.-T. Saito, "Monte Carlo Tree Search in Lines of Action," IEEE Transactions on Computational Intelligence and AI in Games, vol. 2, no. 4, pp. 239-250, 2010.
[21] B. Arneson, R. Hayward and P. Henderson, "Monte Carlo Tree Search in Hex," IEEE Transactions on Computational Intelligence and AI in Games, vol. 2, no. 4, p. 251-258, 2010.
[22] T. Pepels, M. H. M. Winands and M. Lanctot, "Real-Time Monte Carlo Tree Search in Ms Pac-Man," IEEE Transactions on Computational Intelligence and AI in Games, vol. 6, no. 3, pp. 245-257, 2014.
[23] D. J. N. J. Soemers, C. F. Sironi, T. Schuster and M. H. M. Winands, "Enhancements for real-time Monte-Carlo Tree Search in General Video Game Playing," in 2016 IEEE Conference on Computational Intelligence and Games (CIG 2016), pp. 436-443, 2016.
[24] D. Whitehouse, P. Cowling, E. Powley and J. Rollason, "Integrating Monte Carlo Tree Search with Knowledge-Based Methods to Create Engaging Play in a Commercial Mobile Game," in The Ninth AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE 2013), pp. 100-106, 2013.
[25] D. Churchill and M. Buro, "Hierarchical Portfolio Search: Prismata's Robust AI Architecture for Games with Large Search Spaces," in Proceedings of the Artificial Intelligence in Interactive Digital Entertainment Conference, 2015.
[26] M. Sanselone, S. Sanchez, C. Sanza, D. Panzoli and Y. Duthen, "Control of of Non Player Characters in a Medical Learning Game with Monte Carlo Tree Search," in Genetic and Evolutionary Computation Conference (GECCO 2014), pp. 51-52, 2014.
[27] C. Browne, "UCT for PCG," in IEEE Conference on Computational Intelligence and Games (CIG 2013), pp. 1-8, 2013.
[28] A. Goldhoorn, A. Garrell, R. Alquézar and A. Sanfeliu, "Continuous real time POMCP to find-and-follow people by a humanoid service robot," in 14th IEEE-RAS International Conference on Humanoid Robots, Humanoids, Madrid, 2014.
[29] T. P. Runarsson, M. Schoenauer and M. Sebag, "Pilot, Rollout and Monte Carlo Tree Search Methods for Job Shop Scheduling," in 6th International Conference on Learning and Intelligent Optimization (LION 6), pp. 408-423, 2012.
[30] S. Edelkamp, M. Gath, C. Greulich, M. Humann, O. Herzog and M. Lawo, "Monte-Carlo Tree Search for Logistics," in Commercial Transport, Springer International Publishing, 2016, pp. 427-440.
[31] G. Zhu, D. Lizotte and J. Hoey, "Scalable approximate policies for Markov decision process models of hospital elective admissions," Artificial Intelligence in Medicine, vol. 6, no. 1, pp. 21-34, 2014.
[32] Q. Guo, B. An and A. Kolobov, "Approximation Approaches for Solving Security Games with Surveillance Cost: A Preliminary Study," in Issues with Deployment of Emerging Agent-based Systems (IDEAS) Workshop in conjunction with AAMAS 2015, 2015.
[33] D. Hennes and D. Izzo, "Interplanetary Trajectory Planning with Monte Carlo Tree Search," in IJCAI 2015, Buenos Aires, Argentina, 2015.
[34] K. Xiong, H. Jiang, Q. Zhang and M. Zeng, "Monte Carlo Tree Search in Cognitive Opportunistic Spectrum Access and Switch," Journal of Computational Information Systems, vol. 11, no. 18, p. 6571-6579, 2015.
[35] J. van Eyck, J. Ramon, F. Güiza, G. Meyfroidt, M. Bruynooghe and G. den Berghe, "Guided Monte Carlo Tree Search for Planning in Learned Environments," in 5th Asian Conference on Machine Learning (ACML 2013), pp. 33-47, 2013.
[36] F. Golpayegani, I. Dusparic and S. Clarke, "Collaborative, Parallel Monte Carlo Tree Search for Autonomous Electricity Demand Management," in 2015 Sustainable Internet and ICT for Sustainability (SustainIT 2015), pp. 1-8, 2015.
