Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
This follows the much older article "Treebeard - A new way to do Chess" from 2005, which made reference to it using a "Highly directed probability-based tree search". That search was "Interest search", which is now finally described here. This article is also worth reading in conjunction with the last issue's "Searching the Unknown with MCTS", which explores a related methodology ISMCTS that shares some common properties.
Interest Search has proved to be a highly flexible and efficient alternative to conventional minimax and has had a profound impact on AI Factory's flagship games.
A more complete explanation of this method will also appear in the coming AI reference book: "Game AI Pro 2: Collected Wisdom of Game AI Professionals".
Searching in Games
Minimax has been the most important search idea for half a century but, although efficient and effective, it has somehow felt a long way from how humans analyse games. The author here in early days of minimax, working on chess, observed that freezing a minimax search at any point revealed that the current variation being examined was invariably very poor. Even with improved minimax techniques the overall variation quality still generally tended to be very weak.
It seemed wrong that choosing a move to play depended mostly on assessing junk lines of play.
Making Minimax more Human-like
During the early days in the history of computer chess there was a clear division of schools of thought into two camps:
(1) Fast full-width search which attempted to explore all variations, pruned by alpha-beta and related methods to optimize the tree (Shannon type A).
(2) Selective search, which likely spent more time in evaluation, but restricted the number of moves searched through heuristic forward pruning (Shannon type B).
Selective search seemed more "human-like", focussing on more reasonable moves, rather than exploring everything. It looked like it should be the way to go as it could radically reduce the tree size and concentrate more on "good" variations. Selective search had the potential advantage that if it could reliably reduce the number of nodes explored then this could be traded for deeper search. Naturally selective search came at a price, requiring heuristic assessments during search. If the cost of this was less than the saving caused by narrower search, and if this avoided missing moves that should be explored, then selective search could search deeper and therefore be stronger. Since it would also have access to slower evaluation, it would also be able to have better terminal node evaluation.
Hope and logic in those early days suggested that (2) above would win out as the idea of move selection that depended on trying to explore every possible combination of move plays surely could not be the way to deliver the best possible play. However history has shown that method (1) appeared to quickly dominate and the method of forward pruning simply was unable to compete.
Dissecting Selective Search
A problem with selective search is that as soon as you restrict the moves list to some subset, even though the confidence that any one list will have all the moves it needs might be high, that once this gets multiplied in a multi-move variation the risks geometrically increase. Even with a 99% confidence in any one moves list, after 10 plies the chance that the key variation may have been missed is still 10%. To achieve 99% certainty within any one list would alone be very hard and to achieve it would probably mean that there was no selective search saving. You might as well search a few more moves, slightly faster, and be 100% certain that you had examined the key variation.
Selecting by Variation - Interest Search
Returning to the issue of chess spending most of its time examining poor lines, it is easy to see that intuitively wacky moves do not merit the same thorough examination as moves that are more obviously sound.
This is a pointer: dubious moves do not warrant the same level of examination, so that as soon as a variation introduces such a move, the willingness to devote time exploring the variation should diminish.
This is the underlying principle that drives interest search, a focus on the complete variation, not just the move (It should be noted that this principle also drives the selection and expansion phase of MCTS, but not the simulation phase, where most moves are usually selected.)
How Interest Search Works
Interest search passes down a value through the branch indicating how interesting that branch is. A high value means that the variation is already expensive, so low interest, perhaps because it is already deep into the tree or that it includes mediocre moves.
This value is passed down the tree and is used to determine when a branch ends, completely replacing the usual "iterate by depth" by "iterate by interest", where the interest threshold increases with each iteration. Search paths full of highly interesting moves get explored at depth, whereas poor variations are terminated at shallow depths. Once a variation contains one very poor move, it uses up a high proportion of its interest value, so that it only receives limited follow-on search. The same impact might be achieved by a variation containing 2 mediocre moves, which net may generate the same high value of one very poor move. This is intuitively a reasonable idea.
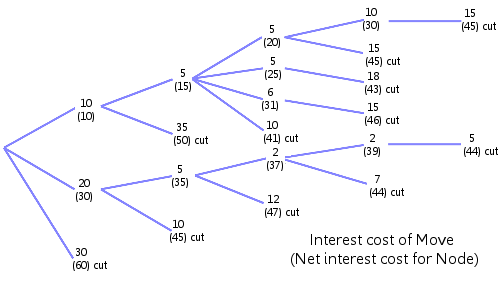
The diagram above shows how this principle works in a tree search, terminated on interest cost rather than depth. The upper number shows the interest cost of that move and the lower number the net interest cost of that branch. As you move left and down the lower number increases in value. When its value exceeds the interest threshold a cut-off occurs.
Linking the Interest Mechanism to Move Values
It would work plausibly well to simply sort the moves into order and apply a cost value linked to the position of the move in the list, so that the first move has a value "1", indicating low cost and the move at the bottom of the list at "30", this would represent high cost.
However we can do much better than that and actually need to link search cost with the likely merit of the move. In our Treebeard chess this delivers a number that corresponds to the interest, where a high value is more interesting, but that for search this is inverted to deliver a "cost", where a high value means high cost = low interest.
This links well into the idea of plausibility analysis, discussed in the article Plausibility Analysis. We can use this analysis, which does not order moves by likely value but by how much we need to look at that move, or that the move will have an easy refutation if bad, so cheap to examine. For example check moves would be pushed to high positions in the move list because, although they may have a low probability of being the right move, they might be very important. If they prove useless then search will quickly reject them.
Using this general principle Treebeard calculates the interest of moves using the following terms:
- Interest is initialized to 1000/number of legal moves
- If in check, value increases +=1000 (function of number of replies)
- Move is in the transposition table +=25
- Ply1 existing previous iteration best move +=100
- Killer move +=100
- Move is voted global "best reply" to previous move in branch += 100
- Best follow-on from previous move 2 plies ago += 100
- Pawn attacks piece +=f(value piece)
- Value of capture +=f(value of capture)
- We give check. +=100, more if our previous ply was also check
- Attack pieces, extra if fork +=f(value of piece)
- Moving a piece under attack +=f(value of piece)
- Capture checking piece +=100
- Promotion +=100
- Diminish interest if beyond iteration depth
- Move piece that is target of pin/tie +=f(value of pin/tie)
- Move is best non-capture +=100
This is used to sum the interest of each move, which is then used to calculate the cost:
The moves list is then sorted by cost, low to high.
At the point that a move may be selected for search, the following calculation is made:
net_cost = total_Path_cost + total_cost_This_Ply + cost_This_Move
where:
| total_Path_cost | Is the net interest cost of the branch leading to this ply. | |
| total_cost_This_Ply | Net interest cost of all previous moves already explored at this ply. | |
| cost_This_Move | The interest cost of the move to be considered. | |
This is then compared to the "iteration interest limit" and if it is greater, then a cut-off occurs and no further moves are explored at this node. This iteration interest limit simply increases the limit for each iteration as each iteration is executed.
Ready to Go?
You may have already figured that this appears to have a serious flaw, and you would be right.
If you test a move that appears to result in a very strong outcome a few plies later, then the opponent could avoid this outcome by exploring a move with a high interest cost, so that it cuts off before the outcome is reached. Indeed this destroys the search, which quickly descends into poor play. The key here is to separate the interest cost tally for different search parities - that is, for each player in the game.
To make this work you need to track separate interest cost for each of the 2 search parities. Now the search cannot avoid an opponent variation outcome by attempting to insert a dull move to force an early cut-off. However this does not stop each side avoiding horizon events. The search could find that a "good" move actually leads to disaster, so avoids the good move by searching a "bad" move that causes an earlier cut-off. This is actually not so different to the existing defect that minimax already has. The difference is that minimax would allow time to be wasted exploring the "bad" move, whereas interest search will cut it off earlier.
Performance with Treebeard Chess
From testing, the addition of interest search resulted in a 20x fold speed-up in search time (500 games), but with only a 41% win rate as there was some inevitable loss of critical moves. If the number of iterations was increased to achieve strength parity, then the net speed-up was 5x fold. See below:
| Player A | Player B | Result for A compared to B | ||
| Time Used | Win % | Comment | ||
| Interest ON | Interest OFF | 20x faster | 41% | |
| Interest ON | Interest OFF | 5x faster | 50% | Re-balanced win rate |
| Interest ON | Interest OFF | Equal time | 72% | Re-balanced time |
Note that this method makes no absolute limit on any one moves list. If the previous branch contained high interest moves then at the current depth there will be the option to potentially explore all moves.
Performance with Shotest Shogi
Although the performance of this with chess was impressive, this method provided the more spectacular savings with our Shogi program Shotest. One reason is that Shogi is a much more combinatorially explosive game, often with up to 200 legal moves in the endgame, so the optimisation proves very effective in radically reducing the tree size.
However interest search was further enhanced for Shogi to penalise searching similar moves at the same ply. For example in Shogi you might be able to play 50 legal drop moves by a Rook, but it does not make sense to try all of these. It is obviously better to order these and try one, but increase the cost of any other drop by the same piece type. This principle can be applied to all kinds of characteristics, for example check moves, so that any one move might be attributed additional cost because it shares a multitude of similar characteristics with previously searched moves.
The net impact of this on Shotest was as follows:
| Player A | Player B | Result for A compared to B | ||
| Time Used | Win % | Comment | ||
| Interest ON | Interest OFF | 119x faster | 8.3% | |
| Interest ON | Interest OFF | 14x faster | 50% | Re-balanced win rate |
| Interest ON | Interest OFF | Equal time | 90.5% | Re-balanced time |
This is clearly a much more impressive performance improvement and almost certainly contributed massively to Shotest's success at the Shogi World Computer Championship, where it twice ranked 3rd in the world. Without interest search it is unlikely it would have managed to do better than the top 30 rankings.
Conclusions
Interest search delivers multiple benefits:
1. Performance
Search is much faster, particularly for combinatorially explosive games. In Shogi this really worked well. In competition, against much more mature programs, they struggled against Shotest when the position became complex, needing to detrimentally reduce the search depth simply to keep within time control. However Shotest was very comfortable, choosing to make the position more complex and managing to easily search deeply.
2. Flexibility
Interest allows iteration by interest threshold, not just depth. This can be dynamic and have any incremental value, however small. This contrasts radically with minimax, which imposes a substantial geometrically increasing and inflexible cost for each extra iteration.
3. Play style
This is arguably the most important input. The search naturally only explores plausible variations similar to what a human might. This does not make it stronger but means the search will not be looking for moves that it can prove are best within the search, as minimax does, but instead make moves (and mistakes) that humans might make. Minimax is a search method, but feels a bit more like a theorem prover than AI.
It should be noted that MCTS and ISMCTS (previous articles) actually share some common characteristics with interest search, particularly "3" above, although the latter methods have problems choosing between overwhelmingly and slightly winning moves, which can lead to odd play.
Finally Treebeard chess was not designed to be the strongest chess program, and indeed would have no chance of beating Shredder, but through interest search it plays a style that people like and is still strong enough to beat 99% of all players at its top level. This is probably why our Chess Free, based on Treebeard, is not only by far the most popular chess on Android, but is also the #1 ranked board game as well.
Our Shotest Shogi would have been lost low in the rankings without interest search, but instead twice ranked #3 in the world and also picked up a Gold medal in the Computer Olympiad. For combinatorially complex games this makes minimax possible where otherwise it was impractical.
All new AI Factory minimax search is now based on interest search.
Jeff Rollason - September 2014
