Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
In previous articles Modular Graphics for Move it!, Solving Deep Puzzles and The Puzzle Workbench we considered the issue of how to analyse and solve puzzles and how to represent these, which was considered in some depth. This article addresses another less obvious, but equally vital topic: how to design puzzles in the first place. It was shown in the articles above that solving deep puzzles can indeed be very hard. However creating the puzzles in the first place also demands effective toolsets.
This article describes how we approached the creation of Move it!.
The Background
As discussed in previous articles, the key to creating puzzles is being able to solve them. This is the single greatest barrier to creating such deep puzzle games, as you need to know whether candidate puzzles can be solved or not.
Having created such a solver, the next question is how to create candidate puzzles that can be solved.
The following considers just the puzzle game Move it! (Move it! Currently ranks #20 among 16,000 competing Android Brain & Puzzle games) and how we approached this.
A Real Puzzle Set
A natural step was to create a physical set that could be used to try out different configurations (below).

The set, held in a plastic envelope, could be pulled out at any time to have a play and look at the puzzle type, so is immediately accessible. This is step one and provided an ideal means to freely experiment with the concept.
However this then requires manual entry of puzzles into the solver in order to test it. If a puzzle does not work, it also encourages you to just tweak the last puzzle tried, just to reduce the time inputting new puzzles. Given that we planned to have >600 puzzles, evidently this was not going to be the development plan.
Switching to on-line Creation
This is obvious, but ideally you must have a puzzle that can be instantly tested as soon as designed, so better to integrate the "play board" directly into the development console.
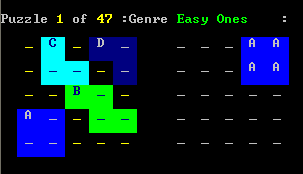
This allows the user to highlight a square and assign either a blank space or the letter of a new shape (note that internally a 3 segment "L" shape is defined by 3 separate cells with the same ID, so that an "L" could be re-edited to create a square etc.)
Once input, pieces can be freely moved around or out of the way to allow other pieces to be added. Once assembled the puzzle can be solved simply by "playing the puzzle". When happy, you click "Solve" to see if the puzzle is solvable and then re-edit if not.
At first glance this, combined with the physical set, looks like it provides much of what you would need. The physical set is still the fastest way to throw together some quick idea and the on-line set the efficient way to get from design to solvable puzzle.
However hands-on designing this way, although it worked, tends to encourage you to design groups of rather similar puzzles. It is so easy to try and re-edit the existing puzzle to create a new one that it tends to undermine some creativity and variation. The first 50 test puzzles were created using this, and they offered a rather narrow range of puzzle designs.
Another defect is simply that the puzzle designs tend to just reflect the limited mindset of the creator, who may have a repeated tendency to explore limited puzzle variations. Finally to get 600 puzzles, with solutions, requires a lot of puzzle throughput and the need to find an efficient route to puzzle creation becomes paramount.
That leads to the next step.
Automated Puzzle creation
At first this might seem to invite the possibility that puzzles could be created on-the-fly within the user app, but for deep puzzles such as Move it! this is pretty well impossible, except for the very simplest of puzzles.
To make automated creation work, it has to provide an easily tuneable framework. If we simply randomly drop pieces onto the puzzle board and just use these, we will probably find we have to wait a long time before it pops up with something that looks like it might be a plausible puzzle.
The solution is to parameterise the probability of each type of object to drop onto the board. Now this is not a probability that the piece will actually be used, but a probability that it will be attempted.
For Move it! we had the following sample parameters:
// zigzag
11 iEmptyCells
0 iHoleInMiddle
0.400 iB1_Bias
0.290 iB2_Bias
0.000 iHoriz2_Bias
0.000 iVert2_Bias
0.050 iB3_Bias
0.000 iHoriz3_Bias
0.000 iB4_Bias
0.000 iSq2x2_Bias
0.010 iL_Bias
0.020 iLS_Bias
0.000 iL3_Bias
0.000 iT_Bias
0.000 iU_Bias
0.040 iZ_Bias
0.010 iLongZ_Bias
0.000 iS_Bias
0.000 ij_Bias
0.000 iH_Bias
0.000 iOT_Bias
0.000 iOL_Bias
0.000 iOZ_Bias
0.000 iD2_Bias
0.000 iD3_Bias
0 iWall
In the example above B1_Bias is a 1x1 block, B2_bias is a 2x1 block and Z_Bias a zigzag shape. The only selected (non zero parameter) shapes here in this case are:
| iB1_Bias | 1x1 block | |
| iB2_Bias | 2x1 or 1x2 Block (2 possible) | |
| iB3_Bias | 3x1 or 1x3 block (2 possible) | |
| iL_Bias | 2x2 L-shape (4 possible) | |
| iLS_Bias | 3x1 or 1x3 long L-shape (8 possible) | |
| iZ_Bias | 2x3 or 3x2 Zig zag (4 possible) | |
| iLongZ_Bias | 3x3 long Zigzag shape (4 possible) |
These parameters are stored in a notebook file and pasted directly into the input parameter command in the testbed, where they are read on-the-fly. This allows the notebook record to accumulate multiple sets of commented parameters that can be edited and copied into the notebook and selectively pasted into the testbed. This allows "favourite" sets of parameters to be marked, re-edited and recovered later.
These are used by simply looping a given grid until the number of required "iEmptyCells" has been satisfied, Each iteration of the loop it runs through the list and uses the given probability to determine whether that shape is to be tried. A single position is tested, and if it fails (piece will not fit), it moves onto the next possible shape and position.
In the case above the top shape is 1x1 block B1_Bias, with a probability of 0.400. That means that there is a 40% chance it will try to drop a 1x1 block before trying something else. Note that not all shapes are equal. The long zigzag shape might be given a probability of 1.00 (100%) of being tried, but it is harder to fit, so will probably fail. The 1x1 block is very easy though.
Once input, the user can simply randomly create a candidate puzzle and either keep requesting new randomised puzzles, or stop to test the last selected one to see if it can be solved.
In practice a puzzle might be plausible, and solvable, but maybe too easy or have some redundant feature. The user can then re-edit the puzzle and try to re-solve it until satisfied.
How well does this work?
Without trying it, it is hard to imagine how well this might succeed. In practice what happens is that by slightly tuning the parameters you detect sweet spots where it generates multiple good puzzles. Tweaked down slightly and suddenly none of the candidate puzzles can ever be solved. Tweaked up and they are all become too trivial to be worth solving.
By juggling between different shapes you can quickly find different and effective ways to combine different types of shape. For certain puzzles you may find that you have to reserve more empty cells, otherwise they are inevitably unsolvable. The ease and freedom of this edit and paste method of controlling the parameters is quick and allows you to mix and match combinations of parameters to find new "sweet" combinations.
Using this is, in practice, not an exercise in engineering methodology but simply a tool that allows you to just randomly experiment. In the wrong hands it might lead to frustration but its flexibility and sensitivity makes it easy to try many different things, so it offers no barriers to those who get in tune with it.
Its key advantage over any implicit direct puzzle design method is that you can easily throw up a wide variety of puzzles that you might never have imagined. You can simply ask the question: "What happens if we combine many zigzags with just a few L shapes?". The generator shows you what this could create and the solver tells you if it is a meaningful solvable puzzle or not.
Evolution of this Framework
The above method has already moved into our new Sticky Blocks game, with enhancements to accommodate the significant added complexity of that game, and will be used for future puzzles as well.
This has been a remarkably useful, simple and effective tool for us.
Jeff Rollason - May 2011
