Copyright Notice: This article is Copyright AI Factory Ltd. Ideas and code belonging to AI Factory may only be used with the direct written permission of AI Factory Ltd.
NOTE! This document has been substantially updated (27 jan 2016) to provide users with some real data, in response to various user requests and inputs.
Unfortunately one common feature shared by essentially ALL backgammon programs is that they are ALL generally accused of cheating. Even the top world-class programs that compete in human competition using real dice attract such claims (see www.bkgm.com/rgb/rgb.cgi?menu+computerdice).
Why is this? Surely these programmers cannot all be knaves, and why should they be? This is not an intellectually difficult game and most reasonably capable games programmers could do a reasonable job to create a viable Backgammon-playing program.
As the reader might imagine, we also have received a deluge of hostile mail accusing our program of cheating, although we have suffered much less than many of our competitors who seem to have been driven to distraction trying to counter these claims. Ironically some of our competitors have stronger Backgammon programs than ours, but this invites even more accusations of cheating.
Whatever our honest intention might be, there is always the potential risk that a program might cheat by accident so we have blocked tested over a million games to check that we have not accidentally cheated and these tests have re-affirmed that the dice rolls appear strictly fair. We also licence out our backgammon game engine and our clients (faced with the same barrage of accusations) have been through our code in fine detail to check, and now confirm, that all was all fair.
We are therefore jumping to our defence and also to the defence of our competitors as well!
This article has a look at this phenomenon. This is not a trivial topic, nor obviously easy to assess as a user.
So why are programs accused of cheating?
This divides into two key reasons:
(a) The impact of large populations of testers
The issue here is that if enough people test, then inevitably someone will eventually see something that appears to be unfair. This section is completely re-written, as it makes for more clarity to go for exact concrete examples.
Looking at our Backgammon analytics we see that each day about 200,000 users play 400,000 Backgammon games. That is an average of 2 games per user per day. If you look at these numbers and try to imagine at what point a user might observe that the program might be cheating, then perhaps they would wait until they had completed 10 games. If we are to test this then we need to run a trial emulating 5 days, which will emulate 200,000 users playing 400,000 x 5 = 2,000,000 games.
That is what we did and these are the results:
A total of 15,286,212 doubles were thrown; 7,639,928 for the emulated player and 7,646,284 for CPU. The CPU received 0.02% more doubles: a very tiny advantage. On average each player saw around 153 doubles in 10 games. If all was fair, you would expect half of these to be your doubles.
However among these 200,000 emulated users, 6,279 of them saw the cpu get 60% or more of the doubles, with player on 40% or less. i.e about 92 doubles for the CPU compared to 61 they received. So the CPU has on or over 1.5x as many doubles. (Note: about the same number saw the reverse, with the player getting 1.5x more doubles). This is exactly what you would expect from a random distribution of doubles.
If this was a single test result, 92 to 61, it would statistically be enough proof of cheating, or some fault. However this is not a single test case!
Here is the crux: over 6000 users will have seen the CPU get many more doubles. If 1% complain then we would expect to see 62 review complaints per day, which is much more than we actually get. (Note this is per day, not per 5 days, as we are looking at the end of a 5 day sequence, so for any one day each user will potentially have just completed a 10 game sequence.)
What if we were actually cheating to this level? If we cheated and only 1% complained, we would receive 2000 cheating complaints per day. Even if only 0.1% complained, then this is still 200 complaints. We get nothing like this.
The conclusion is that we receive the number of complaints we might have expected to receive purely from random chance with a non-cheating program. This is just looking at doubles, but the same argument would apply to any possible cheating.
The core of this problem is that each user cannot see other users. If each user could immediately talk to a random selection of 10 neighbour players they would find that their games overall showed a uniform distribution of doubles.
So the number of complaints we receive is what we would expect from a program that does not cheat.

The end product is an endless stream of outraged players posting angry accusations of cheating. For each such accusation of cheating we do also get a compensating 100x 5-star ratings from many more highly satisfied players, but that is still hundreds of publicly published claims of us cheating.
(b) The deliberate play by the program to reach favourable positions
This reason is much more subtle, but still real and is a key side effect of the nature of the game. Paradoxically, the stronger a program is, the greater the impression is that it might be cheating. This is not because human players are being bad losers but a statistical phenomenon. When you play a strong program you will find that you are repeatedly "unlucky" and that the program is repeatedly "lucky". You will find very often that the program gets the dice it needs to progress while you don't. This may seem like a never-ending streak of bad luck.
Surely this must be cheating??
No, it is not. What is happening is that the program is making good probability decisions. It is making plays that leave its own counters in places where it not only has a high probability that follow-on throws will allow it to successfully continue, but that also obstruct the chance that its opponent will be able to continue.
The net effect is that your dice throws frequently do not do you any good whereas the program happily gets the dice throws it needs to progress.
This may be hard to visualise. After all it is not chess, where a program can exactly know what is going to happen. In backgammon the program does not know what the future dice throws will be, so it needs to assess ALL possible throws that might happen and play its counters with the current dice so that it leaves the best average outcome for all possible future dice throws.
How are these distributions used?
Key to both allowing your counters to get to the squares they need, and blocking opponent plays, is the distribution of dice throws. From schooldays everyone knows that with a single dice all the numbers 1 to 6 have equal probability and that with two dice the most likely throw is a 7, with 6 or 8 next most likely, in a nice symmetrical distribution of probabilities.
However the distribution of likelihood of achieving a value with 2 dice, where you can use either a single dice or both dice, is not so immediately obvious. See below:
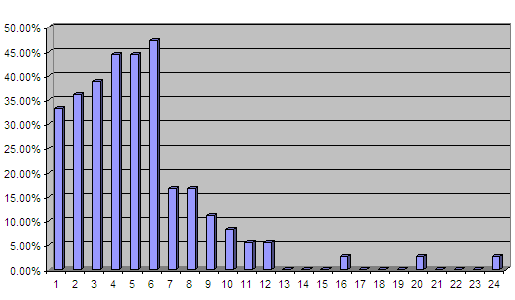
Here the most likely value to achieve is a 6, with 5 next most likely, but 7 is now a low likelihood. Computer Backgammon programs know this and will arrange their pieces such that they are spaced to take advantage of this distribution. A program will not want to put a pair of single counters next to each other but will instead try and put them 6 squares apart.
The overall net effect is that, on average, the program makes good probability choices and will have a better chance of good positions after the next throw, while the human opponent does not.
These good AI choices will mean that your counters are restricted with lower chances of getting dice throws that allow them to move, whereas the program's counters leave themselves on points where they have a high probability of getting a dice throw that allows them to proceed.
This looks like plain "bad luck", but is actually because of good play by your opponent.
Can we prove a program is not cheating by counting up the total number of double and high value dice throws throughout the game?
This is a commonly used defence made of a program, to show that both the AI player and human have had their fair share of doubles and high value throws. However this does not conclusively prove that the AI is not cheating. If there is a serious imbalance, then indeed it must be, but if evenly balanced it might still theoretically be cheating. The program could be taking its doubles when it wants and taking the low throws when it suits it.
Although this might sound a potentially very easy cheat it would actually be very hard to effectively cheat so that it significantly impacted the outcome of the game, without showing an imbalance of throws. In reality this would be very hard to control and it would actually be easier to write a program to play fairly than to cheat effectively like this.
For that reason, AI cheating is very unlikely.
Our backgammon product does display the distribution of dice rolls, so that the user can see that the program is not receiving better dice roll values. Our program also allows the player to roll their own dice and input the amounts, making AI cheating impossible.
Conclusion and External References
The reality is that it is almost certain that all claims of cheating are misplaced and that the appearance of cheating is actually a consequence of so many people playing, inevitably eventually creating some instances of extraordinary luck and also potentially evidence that the program is playing well, making very good probability decisions.
Do not just take our word for it. This is widely discussed in the Computer backgammon world as follows:
# Backgammon Article: which lead to sections addressing why programs
are accused of cheating
http://www.bkgm.com/articles/page6.html
# Computer Dice: http://www.bkgm.com/rgb/rgb.cgi?menu+computerdice
(this sub-link of the above lists discussion of claims of cheating against all the most serious Backgammon programs)
# Computer Dice forum from rec.games.backgammon:
http://www.bkgm.com/rgb/rgb.cgi?view+546
raising the issue of claims of cheating and how to address this.
Jeff Rollason - January 2012
