Copyright Notice: All code and ideas expressed in this article are, by default, Copyright AI Factory Ltd. You may use these, only with the direct written permission of AI Factory Ltd.
This is a follow-on from the earlier article "Driving Search with plausibility Analysis". This article looks at a significantly different approach to plausibility move ordering.
The Main Purpose of Plausibility Analysis
The purpose of Plausibility Analysis is to prioritise moves for tree searching. In the case of non-full width search, this influences which moves get searched, and therefore impacts the final move chosen. For full width search this is more an issue of how quick the search is, taking advantage of the alpha-beta algorithm, which works wonders reducing the tree size. However even in full-width search, plausibility can impact move selection, as it may allow the search to proceed to a deeper iteration.
Pushing Moves up the List
If you read about Plausibility Analysis you will see that the driving idea
is about pushing the right moves to the top of the moves list. This is primarily
to obtain early beta-cutoffs (a beta-cut happens when the search determines
that a branch need not be searched as it can be proven to be redundant). It
is an exercise in probability as the moves are ordered by some likely probability
of success. There are a number of standard techniques for doing this. Typically
the top candidate for this is the hash move choice, as this move has already
been proven in this exact board position before. Much further down the list
come other techniques, such as the History Heuristic, as this uses the much
weaker maxim that "this move has a general good history of working, regardless
of position, so try it again".
Problems with the rush to be looked at first
This therefore becomes an exercise in moves competing for good places in the move selection queue. With simpler games such as Checkers or Chess the number of moves to consider is quite small, so that there are not many moves competing for these top slots. However in games such as Shogi the number of moves can be substantial, in which case the number of moves competing can be huge.
This is where it starts to get difficult. With so many competing moves the competition for move selection is critical. Now "good" moves might get shoved down the list, simply because there are also many other plausible "good" candidates competing.
In our Shogi program Shotest, we have taken a different new approach, as follows:
Penalising dud moves
The problem with any heuristic method for ordering moves for plausibility is that sometimes useless moves can get a very good plausibility score. In consequence these dud moves elbow their way near the top of the list, even though they might never succeed. The maxim then becomes "this move looks very promising, so let's try it again (even though in the last 100,000 attempts it failed!)". In Shogi this could easily be very common as drops offer huge numbers of promising-looking moves.
What is needed is a means of also having a traffic of moves being pushed down the list as well as moves being pushed up. Moves that look good, but repeatedly fail, need to be penalised.
The Penalty System
You need to establish a criteria for "failure". This is not as obvious as it might look. Success is easy: You only need to spot a beta-cutoff to detect a successful move, but all the moves that did not cause a beta-cutoff are not necessarily bad moves.
After experimentation, the following scheme was adopted:
The search maintains a table with a penalty value for all possible moves. Whenever a beta-cut is detected, then all moves searched before that beta-cut may have been over-valued. The search then penalises these moves, depending on the distance in move position between the beta cut and that move. I.e. if the cut occurred at move 20, then the first move is penalised by 19 points, but the 18th move by only 2 points. During plausibility selection the penalty is used to penalise the selection of that move. This table is also aged between each iteration, halving the values in the table. This prevents an early bad track record undermining a move that may later become good.
Example in Use
The following is a sample position reached in one of our Shogi program Shotest games against the program Spear:
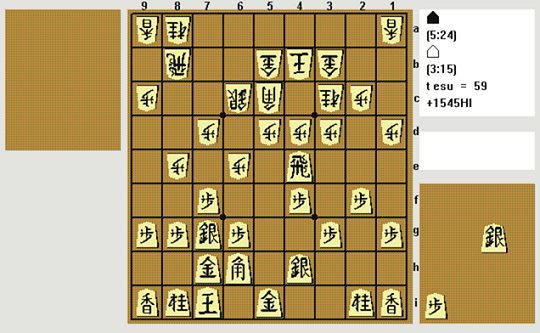
Shotest is black (Sente) playing down the board. This position came to our attention as Shotest played N8a-7c instead of the expected P4dxR4e. As it happens N8a-7c is not as bad as it might first appear, because the rook cannot escape.
However, examining the search, this demonstrates the negative plausibility in action. Examining the branch from this position after the moves:
| 60. | N 3cx4e | |||||||
| 61. | P 4fx4e | |||||||
| 62. | P 4dx4e | |||||||
| 63. | N * 5g | |||||||
| 64. | B 5cx2f | |||||||
We then reach the position below:
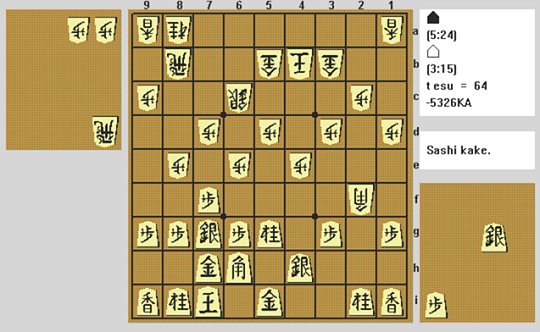
From this position a very likely choice should be N5gxP4e. However, without negative plausibility, the plausibility analysis (with the help of move selection heuristics, killer moves and other such techniques) gave the following list of moves:
| 1. | P * 4c | |||||||
| 2. | S * 2g | |||||||
| 3. | N 5gx6e | |||||||
| 4. | P * 2g | |||||||
| 5. | S * 3c | |||||||
| 6. | P * 5c | |||||||
| 7. | S * 5c | |||||||
| 8. | P 6g-6f | |||||||
| 9. | P * 4f | |||||||
| 10. | S * 4c | |||||||
| 11. | P * 4d | |||||||
| 12. | P * 2d | |||||||
| 13. | S * 2a | |||||||
| 14. | S * 3a | |||||||
| 15. | P * 2b | |||||||
| 16. | N 5gx4e | |||||||
Here the otherwise favoured move N 5gx4e does not get considered until move 16. This unnaturally low position is because the alternative N 5gx6e was slightly favoured and then, having considered this move, the alternative similar capture is less interesting to consider. The other moves here that get looked at first are various dangerous moves. However these are largely ineffective.
With negative plausibility the list changes as follows:
| 1. | S * 2g | |||||||
| 2. | N 5gx4e | |||||||
| 3. | P * 2g | |||||||
| 4. | P * 5c | |||||||
| 5. | S * 5c | |||||||
| 6. | N 5gx6e | |||||||
| 7. | ... | |||||||
Now the favoured move has moved to the second position. This is because the various other "dangerous" moves have proven ineffective in earlier searches, so that they get penalised. N 5gx4e even moves ahead of its similar N 5gx6e as the latter must have received a penalty elsewhere.
Conclusion
This technique is attractive as it corrects for any positive errors in the existing plausibility analysis. It does not spot neglected underrated moves, but does remove overrated moves from the list. This is attractive as it is done without any game-specific heuristics. In the example above the plausibility analysis actually did a bad job of selecting moves (a failing that will be rectified in the coming Shotest!), but this did not cause a critical failure, as the negative plausibility demoted the futile overrated moves.
Of course this is only good if it means an improved performance. Initial testing of this with Shotest against a version without negative plausibility shows the following result:
| Games | Wins | Losses | %Win | %Loss |
| 474 | 268 | 206 | 56.5% | 43.5% |
This was for games where each side had 25 minutes to play all its moves (standard CSA time). It may not look dramatic, but applying this to the binomial distribution, this gives the following figures:
| Population n=474, a : b 268 : 206 'p' calculated from a/n is 0.5654 | ||||||
| The probability that A > B (p>q) is 0.997802 | ||||||
| and that A < B (p<q) is 0.002198 | ||||||
| p=0.998 expressed as a fraction/ratio is ( 454.0 : 1 ) | ||||||
| Results 268 + 206 give the following range of values for 'p' (as %) within 0.01% | ||||||
| 'p' within 50% probability within range 55.0% <-- 56.5% --> 58.1% | ||||||
| 'p' within 67% probability within range 54.4% <-- 56.5% --> 58.7% | ||||||
| 'p' within 95% probability within range 52.0% <-- 56.5% --> 60.9% | ||||||
| 'p' within 99% probability within range 50.6% <-- 56.5% --> 62.3% | ||||||
| 'p' 99% probability higher than 51.2% | ||||||
| 'p' 95% probability higher than 52.8% | ||||||
| 'p' 67% probability higher than 55.5% | ||||||
| 'p' 33% probability higher than 57.5% | ||||||
| 'p' 10% probability higher than 59.4% | ||||||
| 'p' 5% probability higher than 60.2% | ||||||
| 'p' 1% probability higher than 61.8% | ||||||
From these figures the indication is that statistically this provides 99.8% confidence that it resulted in an improved performance, and 95% probability that the strength is at least a 52.8% win rate.
As other aspects of Shotest are improved, this technique may yield a greater advancement in performance, as greater weaknesses are first eliminated.
In conclusion this provides a generic technique that can equally well be applied to any tree-searching game, with a particular advantage for games with many legal moves.
Jeff Rollason: March 2007
