---

Copyright Notice: All code and ideas expressed in this article, are Copyright AI Factory Ltd.
You may use these, only with the direct written permission of AI Factory Ltd.

---

A common feature of many game engines that use tree search is the need to search out a position to find a "quiet" position before evaluating. This is not necessary with games like Reversi/Othello, as most positions can generally be equally well assessed statically. Therefore such engines can search to a given depth and then evaluate at that fixed depth. In chess this is not very practical. For example, searching to depth of 6 moves where the last move is rook-takes-rook cannot be assessed as leaving one side a rook up, unless you know that a recapture is not possible. Therefore in chess the evaluation needs to determine what the outcome of any outstanding captures is. This could be by statically assessing the possible exchanges remaining, but this is quite hard, and another easier and more accurate solution is available. This is "capture" or "quiescence" search. This completes a conventional search and then does a fast quiescence search to simply determine the outcome of outstanding captures. This works well, as captures sequences generally simplify very quickly. In consequence most chess programs determine the material balance of a position by evaluating at the end node and then performing a quiescence search to determine captures.

Quiescence and Shogi

Unlike chess, shogi offers a difficult challenge to dealing with quiescence. The main problems are as follows:

1. Value of Pieces

Unlike chess, in shogi the value of pieces is variable and overlaps with positional evaluation. Therefore separating out material values assessed using quiescence, and then positional features using fixed depth, does not work that well. A piece may radically change its value, depending on its position on the board. In some instances a piece can lose most of its value within just a few moves.

2. Positions do not simplify

This is the killer characteristic of shogi that makes quiescence search very difficult. In chess as captures are followed through, the position rapidly simplifies. In shogi any piece that is captured becomes available for a drop (a piece can be re-played on the board in any position). A piece that can drop generally offers more possibilities for tactical moves, simply because it can reach any square. Therefore following some capture sequence does not result in easy simplification.

A further complication is that in Shogi the late middlegame and endgame positions commonly leave large numbers of pieces hanging. This can be shown by examining some example shogi games. The table below looks at the number of squares where a profitable capture or tactical move (including promotions and forks) can be made, starting from move 50 to avoid the quiet opening phase. This uses a sample of 10 games played between two Shogi programs.

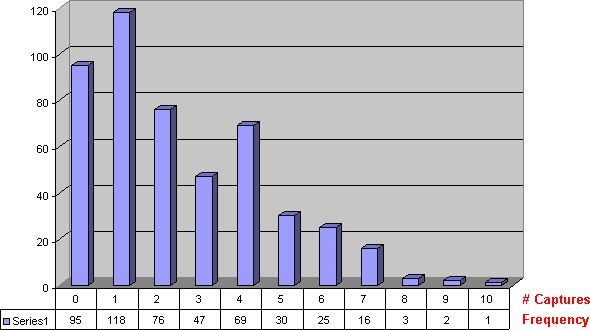
From this it can be seen that in 80% of the positions here there are profitable captures. Over 55% of the positions have 2 or more captures and 30% have 4 or more. This contrasts sharply with Chess where probably less than 10% of positions have profitable captures and positions with 2 or more are relatively rare.

A Shogi evaluation should therefore normally expect to have pieces hanging, so that looking for a search to just simplify this is not practical.

Our shogi program "Shotest" takes a radical approach to solving this, as follows:

Solving Tactical Positions Without Search

1 Basic goals of SUPER-SOMA

The SHOTEST Shogi program does not use tree search to resolve tactical exchanges. It instead uses a static evaluation to assess tactical threats, without search. In practice this is inevitably very hard and to make this a complete alternative to search would be almost impossible. Instead the search supplements such an evaluation. A tactical exchange may therefore be predominately assessed using static evaluation, but with a significant search component, rather than the conventional solution where search is responsible for determining tactical exchange values. The static tactical evaluation also controls when search may be required by identifying that the position is either too complex to make a reliable evaluation, or that a particular critical component is present.

Finally tactical threats do not just include captures, but also defensive moves, promotion, checks, mate threats and forks. For this static assessment of tactical exchanges to work it needs to be able to predict all kinds of tactical moves.

2 Operation of SUPER-SOMA

This text assumes that the reader is familiar with the idea of simple swap-off algorithms for determining the values of captures on single squares. This mechanism first appeared in the chess program SOMA, and is used in many Chess programs. It determines the point at which an exchange stops on a square, perhaps with no exchange occurring. It initially assumes that a complete exchange will occur and then iteratively each side can choose to stop the exchange earlier by not making an exchange, until neither side can improve the result.

SUPER-SOMA makes an immediate improvement to this by taking pins and ties into account in this swap-off. This algorithm is quite complex, so it needs a fairly complete description. In the following examples the values of the pieces are assumed to be:

	(P)Pawn	(L)Lance	(N)Knight	(S)Silver	(G)Gold	(B)Bishop	(R)Rook	(K)King
	52	120	120	200	220	360	480	3999
	the following pieces are the promoted forms of the pieces above
	P+	L+	N+	B+	R+
	240	230	230	460	550

The following board example shows a position where a piece is tied:

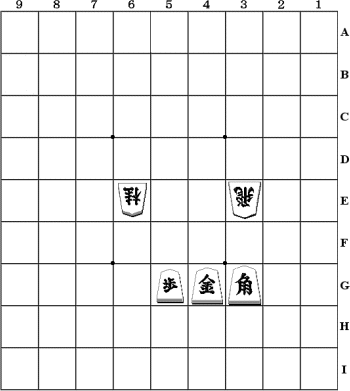
For those not familiar with the piece notation, this shows a white knight (N 6e), white rook (R 3e), black pawn (p 5g), black gold (g 4g) and black bishop (b 3g). . In this the Gold (G) is tied to protecting both the Pawn and Bishop. The reader is referred to Wikipedia for details of the moves.

Considering square 5g we have the exchange:

Nxp +52

Treating this as a simple SOMA exchange it is easy to see that no profitable capture is possible. However the Gold on 4g is tied to defending the Bishop on 3g, which is attacked by the Rook on 3e. The value of the tie is 360 points, the value of the Bishop. If this is incorporated into a conventional SOMA exchange we have:

Nxp +52

The consequence of this is that black's final move gxN leaves black with a net loss of 308 points, which is worse than no recapture. Applying the SOMA principle the exchange ends with Nxp with a net gain of 52 points for white. The tie to protecting the bishop has prevented the re-capture.

This is the basic unit used by SUPER-SOMA. The full mechanism allows tactical exchanges to account for multiple tactical moves on the board, which are inter-related. The basic structure of this is as follows:

A.	Generate the table "XREF" to contain a list of tactical moves
	A1.	Do a basic scan to determine all attacks on all squares.
	A2.	Identify all pins, ties and discovered attacks. These would include ties to defending material, prevention of promotion and threats of mate.
	A3.	Create the table XREF with all exchanges on the board. This would use a variant of SOMA that would understand where pieces are pinned tied or activate discovered attacks.
	A4.	Add further threats to XREF including forks, attacks on immobile pieces and promotions.
B.	Apply SUPER-SOMA to XREF
	B1.	Apply an initial weight to each XREF entry depending on its expected net value as an isolated tactical move
	B2.	Cross reference each XREF entry, applying an enhanced weighting for each table entry based on its influence on other XREF entries. e.g. The move BxP might have the initial weight of one pawn, but if the bishop is also vulnerable to capture, then the BxP entry would be weighted as value of pawn+bishop.
	B3.	Choose the best move from XREF for the side to play next. This might be a capture, promotion, fork or even a move to neutralise an opponent's threat. If there are no moves with a positive weighting then generate a "pass" move.
	B4.	Update the XREF table after making the move, and change the side to play (if appropriate).
	B5.	Repeat from step (B1) until both sides have played a pass move.

This complete process is quite complex. The following section describes its use in a simple example.

Whole board analysis using SUPER-SOMA with the XREF table

This example assumes white is to play next:

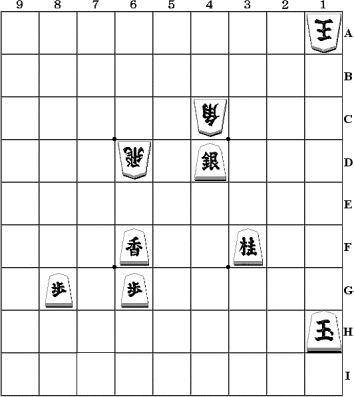
In the example diagram below SUPER-SOMA finds 6 moves for the XREF table, as follows:

	Move		Value	Type of Move
	l	6fxR6d	960	capture
	s	4dxB4c	740	capture and promote
	R	6dxs4d	-560	capture
	R	6dxl6f	-720	capture
	B	4cxp8g	152	capture and promote
	s	4d- 5c	20	promote

From this we can see that the greatest value move is L 6fxR6d with an exchange value of 960 points (value of black losing rook plus value of white gaining rook in hand). This is a move for black though and white is to play next. White's most valuable move is the capture and promotion move B 4cxp8g. White's other moves are R 6dxl6f which lose a Rook for a Lance and R 6dxs4d losing a Rook for a Silver, so both have negative values.

If you apply SUPER-SOMA to this position it predicts the following move sequence:

	R	6dxs4d	500
	n	3fxR4d	960
	B	4cxp8g	152
		pass
		pass		Net value -408

SUPER-SOMA has predicted that the best move is the sacrifice of the Rook for the Silver. In Shogi terms this makes sense as simply moving the Rook away from the threat by the lance will result in black then capturing the Bishop with the Silver, whereas sacrificing the Rook for the Silver also prevents the capture of the Bishop, so this is the correct result.

We can look to see how SUPER-SOMA does this.

1 First Iteration of SUPER-SOMA

The following is the table XREF used by Shotest as it would appear after the first step "B3" above. It needs some explanation:

BDRI+SRDX	Move	Value	1st	Recapture	Neutralise	Weight
--r--s--x	l 6fxR6d	960	960	0	Yes	960
--r--s--x	s 4dxB4c	740	740	0	Yes	944
--r--s--x	R 6dxs4d	-560	400	-960		1160
--r--s--x	R 6dxl6f	-720	240	-960		240
--r--s--x	B 4cxp8g	152	152	0		982
-d---s--x	s 4d- 5c+	20	20	0	Yes	20

Key for table XREF:

The header BDRI+SRDX below shows "-" for "off" and lowercase letter for "on"

B = Threat can be blocked

Val = Net value of exchange

From the table above we can see how the top weighted move is R 6dxs4d with 1160 points, despite its low initial value. If we examine the cross-referencing that occurred in step "B2" we can understand how this value was derived.

	Step B2: Cross-referencing of table
	B	4cxp8g	gives	152	to	s	4dxB4c	capturing piece is our target
	l	6fxR6d	gives	960	to	R	6dxs4d	our piece is target of other capture
	s	4dxB4c	gives	740	to	R	6dxs4d	capturing piece is our target
	s	4d -5c	gives	20	to	R	6dxs4d	capturing piece is our target
	l	6fxR6d	gives	960	to	R	6dxl6f	our piece is target of other capture
								capturing piece is our target
	s	4dxB4c	gives	740	to	B	4cxp8g	our piece is target of other capture

The first choice is R 6dxs4d as previously indicated, but the second choice is to simply neutralise the move l 6fxR6d by moving the Rook away. The first "R" column is marked by "r" indicating that the Rook can safely run and so this neutralising move is possible. In some cases a threat cannot be fully neutralised, e.g. if the piece has no safe squares then it may simply need to be defended. This might prevent the capture, or may just allow re-capture of the attacking piece, for example LxR above could be defended by a pawn drop behind the Rook. This would not stop the loss of the Rook, but would allow capture of the Lance in compensation. This partial defence would be reflected in the cross-reference weighting given.

The third choice above is the initially positive capture B 4cxp8g.

SUPER-SOMA will therefore predict the move R 6dxs4d above and proceed to step "B4" to update the table.

2 Second Iteration of SUPER-SOMA.

After step B4 above and iterating B1, B2 and B3 again, the XREF will now contain the following:

BDRI+SRDX	Move	Value	1st	Recapture	Neutralise	Weight
--r--s--x	n 3fxR4d	960	960	0		960
--r--s--x	B 4cxp8g	152	152	0	Yes	152

Four of the table entries have gone as they are now void, for example the capture s 4dxB4c is no longer possible as the Silver has been captured.

Black is now the side to play. There are only two moves and these are not linked. Black can either neutralise the capture B 4cxp8g by moving the pawn or capture the Rook on 4d. The latter has a much higher weight and so is chosen.

3 Third Iteration of SUPER-SOMA

After n 3fxR4d the table contains just one move, as follows:

BDRI+SRDX	Move	Value	1st	Recapture	Neutralise	Weight
--r--s--x	B 4cxp8g	152	152	0	Yes	152

This move has a positive value and is selected.

After this move both black and white will play pass moves and the sequence ends.

4 Discussion of Example

The example above is simple, but demonstrates the basic mechanism of SUPER-SOMA. A more complex example could include assessments of defensive moves, pins, ties, mate threats, forks and promotions. For example: A piece may be tied to protecting a square where mate could occur. A piece that was under attack might have no safe square, but could run to a square where a re-capture was possible. A piece might also be vulnerable to a fork, in which case the piece could run to a square that avoids the fork. However the example above was complex enough to show the principle.

Conclusion

If you read this far, then you will appreciate that this was a heavier-than-average article! This technique is not easy to implement, but has proven effective at handling the problem of capture sequences that do not easily simplify.

This has been used in SHOTEST for 9 years. In competition SHOTEST typically examines search trees some 20 times smaller than rival programs, but this tactical mechanism has allowed it to still perform well against all the top programs that use conventional Chess techniques. It has twice come 3rd in the rankings, among some 50 rival programs.

This is an ideal game type for such a mechanism, so has proved a good testbed to develop it.

Jeff Rollason - December 2006

Further reading:

"SUPER-SOMA – Solving tactical exchanges in Shogi without tree searching”, paper for CG2000 Hamamatsu 2000, Springer-Verlag.
“Computer Shogi” chapter in “Artificial Intelligence” co-authored with Prof. Hiroyuki Iida
“SUPER-SOMA - Whole board static capture exchange evaluator for Shogi” chapter in “Advances in Computer Shogi”, publ Kyoritsu
“Chips Challenging Champions” – Chapter on “Computer Shogi” with M. Sakuta and H. Iida Elsevier ISBN 0 444 50949 6

Home What's New! Articles Listing Article: Looking for Alternatives to Quiescence Search Article: Intelligent Diagnostic Tracing The 3rd Party Engine Resource Custom AI for 3rd Parties Quality 3D Products Links AI Factory website